题目内容
如图所示为圆柱形大型储油罐固定在U型槽上的横截面图.已知图中ABCD为等腰梯形(AB∥DC),支点A与B相距8 m,罐底最低点到地面CD距离为1 m.设油罐横截面圆心为O,半径为5 m,∠D=56°,求:U型槽的横截面(阴影部分)的面积.(参考数据:sin 53°≈0.8,tan 56°≈1.5,π≈3,结果保留整数)
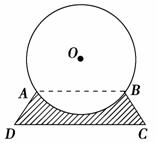
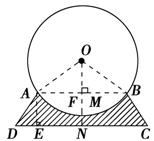
解 如图,连接A O、BO.过点A作AE⊥DC于点
O、BO.过点A作AE⊥DC于点 E,过点O作ON⊥DC于点N,ON交⊙O于点M,交AB于点F,则OF⊥AB.
E,过点O作ON⊥DC于点N,ON交⊙O于点M,交AB于点F,则OF⊥AB.
∵OA=OB=5 m,AB=8 m,
∴AF=BF=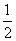 AB=4(m),∠AOB=2∠AOF,在Rt△AOF中,sin∠AOF=
AB=4(m),∠AOB=2∠AOF,在Rt△AOF中,sin∠AOF=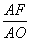 =0.8=sin 53°,
=0.8=sin 53°,
 ∴∠AOF=53°,则∠AOB=106°,
∴∠AOF=53°,则∠AOB=106°,
∵OF=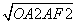 =3(m),由题意得:MN=1 m,
=3(m),由题意得:MN=1 m,
∴FN=OM-OF+MN=3(m ),
),
∵四边形ABCD是等腰梯形,AE⊥DC,FN⊥AB,
∴AE=FN=3 m,DC=AB+2DE.
在Rt△ADE中,tan 56°=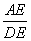 =
=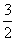 ,
,
∴DE=2 m,DC=12 m.
∴S阴=S梯形ABCD-(S扇形OAB-S△OAB)=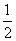 (8+12)×3-
(8+12)×3-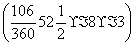
≈20(m2).
答 U型槽的横截面 积约为20 m2.
积约为20 m2.

练习册系列答案
相关题目
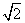 cm的正方形ABCD中,E,F是对角线AC上的两个点,它们分别从点A、点C同时出发,沿对角线以1 cm/s的相同速度运动,过E作EH垂直AC,交Rt△ADC的直角边于H;过F作FG垂直AC,交Rt△ADC的直角边于G,连接HG,EB. 设HE,EF,FG,GH围成的图形面积为S1,AE,EB,BA围成的图形面积为S2(这里
cm的正方形ABCD中,E,F是对角线AC上的两个点,它们分别从点A、点C同时出发,沿对角线以1 cm/s的相同速度运动,过E作EH垂直AC,交Rt△ADC的直角边于H;过F作FG垂直AC,交Rt△ADC的直角边于G,连接HG,EB. 设HE,EF,FG,GH围成的图形面积为S1,AE,EB,BA围成的图形面积为S2(这里 规定:线段的面积为0).若E到达C,F到达A
规定:线段的面积为0).若E到达C,F到达A
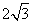 cm B.
cm B. cm
cm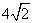 cm D.
cm D.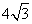 cm
cm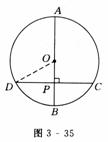


 中国共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是( )
中国共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是( )
 上,则∠C的度数是________-.
上,则∠C的度数是________-.
