Question

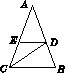
已知：如图15，锐角△ABC的两条高BD、CE相交于点O，且OB=OC.

（1）求证：△ABC是等腰三角形；

 

（2）判断点O是否在∠BAC的平分线上，并说明理由.

Answer 1

（1）证明：如答图5，∵OB=OC,∴∠OBC=∠OCB,∵BD、CE是两条高,∴∠BDC=∠CEB=

90°,又∵BC=CB ，∴△BDC≌△CEB（AAS），

∴∠DCB=∠EBC,∴AB=AC,∴△ABC是等腰三角形.

（2）解：点O在∠BAC的平分线上.如答图5，连接AO.

 

答图5

∵ △BDC≌△CEB,∴BD=CE,又∵OB=OC,∴ OD=OE.

又∵∠BDA=∠CEA=90°,AO=AO,∴Rt△ADO≌Rt△AEO（HL）,

∴∠DAO=∠EAO，∴点O在∠BAC的平分线上.