Question

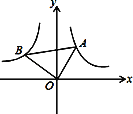
【题目】如图，抛物线经过点，，与轴正半轴交于点，与轴交于点.

(1)求直线的解析式；

(2)设点为直线下方抛物线上一点，连接、，当面积最大时，求点的坐标；

(3)在(2)的条件下，直线过直线与轴的交点.设的中点为，是直线上一点，是直线上一点，求周长的最小值.

Answer 1

【答案】（1）y=2x-3（2）当时，有最大值，此时P(2，-3)（3）

【解析】分析：(1)把点A的坐标代入中求出二次函数的解析式，得点C的坐标，用待定系数法求AC的解析式；(2)设，则过P作轴的平行线与AC的交点坐标为，用含x的式子表示出，结合二次函数的性质求解；(3)判断点F关于CP的对称点Q的坐标，关于直线的对称点是原点O，则△EHF的周长的最小值是OQ的长.

详解：(1)…

(2)设，则过P作轴的平行线与AC的交点坐标为，

.

所以当x＝2时，有最大值，此时P(2，－3)

(3)B(3，0)，C(0，－3)，则，F关于PC的对称点为

直线过D(，0)，所以直线的解析式为，

所以F点关于直线的对称点为原点，

所以△EHF的周长的最小值为OQ的长，

根据勾股定理得，OQ＝ ＝.