题目内容
 如图,已知△ABC的三边长为别为5,12,13,分别以三边为直径向上作三个半圆,则图中阴影部分的面积为
如图,已知△ABC的三边长为别为5,12,13,分别以三边为直径向上作三个半圆,则图中阴影部分的面积为考点:勾股定理
专题:
分析:先利用勾股定理逆定理求出△ABC是直角三角形,再根据图形,阴影部分的面积等于两个小扇形的面积加上△ABC的面积减去大扇形的面积,然后列式计算即可得解.
解答:解:∵52+122=169=132,
∴△ABC是直角三角形,
由图可知,阴影部分的面积=
π(
)2+
π(
)2+
×5×12-
π(
)2,
=
π+
π+30-
π,
=30.
故答案为:30.
∴△ABC是直角三角形,
由图可知,阴影部分的面积=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 12 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
=
| 25 |
| 8 |
| 144 |
| 8 |
| 169 |
| 8 |
=30.
故答案为:30.
点评:本题考查了勾股定理,扇形的面积,观察图形,表示出阴影部分的面积是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
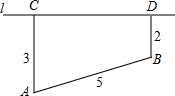 已知,河岸l同侧有A、B两镇,A、B到L的距离CA=3,BD=2,AB=5,在l上找一点P,使PA=PB.
已知,河岸l同侧有A、B两镇,A、B到L的距离CA=3,BD=2,AB=5,在l上找一点P,使PA=PB. 如图,⊙O的直径AB和弦CD相交于点E,AE=2,EB=5,∠DEB=30°,求弦CD的长.
如图,⊙O的直径AB和弦CD相交于点E,AE=2,EB=5,∠DEB=30°,求弦CD的长. 如图所示,AB、CD相交于点O.OB平分∠DOE,若∠DOE=63°12′,则∠AOC的度数是
如图所示,AB、CD相交于点O.OB平分∠DOE,若∠DOE=63°12′,则∠AOC的度数是 如图,点A(3,0)、B(0,4)、C(-2,0),将△ABC沿AB对折得△ABD,双曲线y=
如图,点A(3,0)、B(0,4)、C(-2,0),将△ABC沿AB对折得△ABD,双曲线y=