题目内容
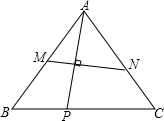如图，设P是等边△ABC的一边BC上的任意一点，连接AP，它的垂直平分线交AB、AC于M、N两点，求证：BP•PC=BM•CN．
分析：连接PM，PN，证明△AMN≌△PMN，再证△MPB∽△PNC，即可得出结论．
解答：
证明：连接PM，PN，
∵MN垂直平分AP，
∴AM=MP，AN=PN，又MN为公共边，
∴△AMN≌△PMN（SSS），
∴∠MPN=∠BAC=60°，
∵∠BPM+∠CPN=120°，∠BPM+∠BMP=120°，
∴∠BMP=∠CPN，
由∠B=∠C=60°，
∴△MPB∽△PNC，
∴
=
，
即BP•PC=BM•NC．
证明：连接PM，PN，∵MN垂直平分AP，
∴AM=MP，AN=PN，又MN为公共边，
∴△AMN≌△PMN（SSS），
∴∠MPN=∠BAC=60°，
∵∠BPM+∠CPN=120°，∠BPM+∠BMP=120°，
∴∠BMP=∠CPN，
由∠B=∠C=60°，
∴△MPB∽△PNC，
∴
| BP |
| NC |
| BM |
| PC |
即BP•PC=BM•NC．
点评：本题主要考查了相似三角形的判定及性质以及等边三角形的性质等问题，能够熟练掌握．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
12、如图，设P是等边三角形ABC内任意一点，△ACP′是由△ABP旋转得到的，则PA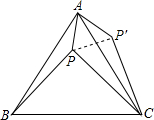
（按课改要求命制）如图，设P是等边三角形ABC内的一点，PA=1，PB=2，PC=
3、如图，设P是等边△ABC内的一点，PA=3，PB=4，PC=5，则∠APB的度数是
22、如图．设P是等边△ABC内的一点，且PA：PB：PC=3：4：5，求∠APB的度数．