题目内容
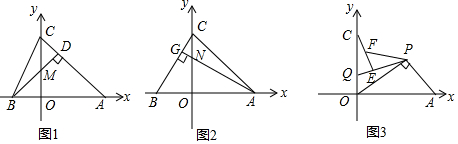
6.如图,△ABC中,A(a,0),B(b,0),C(0,c),且满足b=$\sqrt{a-c}$+$\sqrt{c-a}$-2,(1)BD⊥AC于D,交y轴于M,求M点坐标;
(2)过点A作AG⊥BC于G,交OC于N,若∠CAN=15°,求AN的长;
(3)P为第一象限一点,PQ⊥PA交y轴于Q.在PQ上截取PE=PA,F为CE的中点,求∠OPF的度数.
分析 (1)先判定△AOC是等腰直角三角形,再判定△BOM是等腰直角三角形,根据OB=2,得出OM=2,即可得出M(0,2);
(2)先求得∠BCO=∠OAN=30°,再判定△BOC≌△NOA(ASA),得到BC=NA,再根据Rt△BOC中,BC=2BO=4,即可得出AN=4;
(3)先连接OF,把△OCF绕点O顺时针旋转90°至△OAD处,连接DP,由旋转可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,再判定△PEF≌△PAD(SAS),得出PF=PD,∠FPE=∠DPA,进而判定△OPF≌△OPD(SSS),即可∠OPF=∠OPD=$\frac{1}{2}$∠FPD=45°.
解答 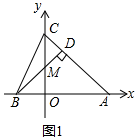 解:(1)由题可得,a-c≥0,c-a≥0,
解:(1)由题可得,a-c≥0,c-a≥0,
∴a=c,即OA=OC,
∴△AOC是等腰直角三角形,
∴∠OAD=45°,
又∵BD⊥AC,
∴∠ABD=45°,
又∵∠BOM=90°,
∴△BOM是等腰直角三角形,
∴OB=OM,
∵b=$\sqrt{a-c}$+$\sqrt{c-a}$-2,且a=c,
∴b=-2,即OB=2,
∴OM=2,
∴M(0,2);
(2)∵∠CAN=15°,∠OAC=45°,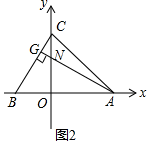
∴∠OAN=30°,
∵AG⊥BC,CO⊥AO,∠ANO=∠CNG,
∴∠BCO=∠OAN=30°,
在△BOC和△NOA中,
$\left\{\begin{array}{l}{∠BCO=∠OAN}\\{CO=AO}\\{∠COB=∠AON}\end{array}\right.$,
∴△BOC≌△NOA(ASA),
∴BC=NA,
又∵Rt△BOC中,BC=2BO=4,
∴AN=4;
(3)如图3,连接OF,把△OCF绕点O顺时针旋转90°至△OAD处,连接DP,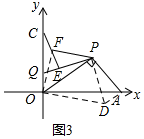
由旋转可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,
∵∠AOQ+∠APQ=180°,
∴∠OAP+∠OQP=180°,
又∵∠EQC+∠OQP=180°,
∴∠OAP=∠EQC,
∴∠PEF=∠PAD,
在△PEF和△PAD中,
$\left\{\begin{array}{l}{EF=AD}\\{∠PEF=∠PAD}\\{PE=PA}\end{array}\right.$,
∴△PEF≌△PAD(SAS),
∴PF=PD,∠FPE=∠DPA,
∴∠FPD=∠QPA=90°,
∵在△OPF和△OPD中,
$\left\{\begin{array}{l}{OF=OD}\\{OP=OP}\\{PF=PD}\end{array}\right.$,
∴△OPF≌△OPD(SSS),
∴∠OPF=∠OPD=$\frac{1}{2}$∠FPD=45°.
点评 本题属于三角形综合题,主要考查了全等三角形的判定与性质,等腰直角三角形的性质,旋转的性质以及二次根式有意义的条件的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形对应相等,对应角相等进行计算求解.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案| A. | -6 | B. | -9 | C. | 9 | D. | 6 |
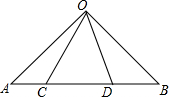 如图,在Rt△AOB中,∠AOB=90°,OA=OB=4,点C、D在边AB上,且∠COD=45°,设AD=x,BC=y.
如图,在Rt△AOB中,∠AOB=90°,OA=OB=4,点C、D在边AB上,且∠COD=45°,设AD=x,BC=y.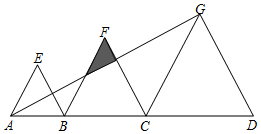 如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则
如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则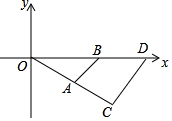 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为(1,-1).
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为(1,-1).