题目内容
17.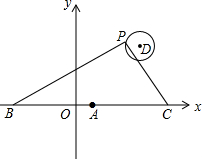 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最小值是4.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最小值是4.
分析 利用点A、B、C的坐标可得到AB=AC=a,则AB=AC=AP=a,连接AD交⊙D于P′,利用两点间的距离公式计算出DA=5,即可得到P′A=4,于是可判断a的最小值为4.
解答 解:∵点A(1,0),B(1-a,0),C(1+a,0),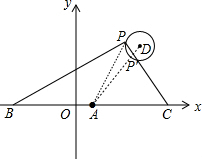
∴AB=AC=a,
∵∠BPC=90°,
∴AB=AC=AP=a,
连接AD交⊙D于P′,
DA=$\sqrt{(4-1)^{2}+{4}^{2}}$=5,
∴P′A=5-1=4,
即⊙D上点到A的最短距离为4,
∴a的最小值为4.
故答案为4.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了坐标与图形性质.

练习册系列答案
相关题目
7.已知x与y之间的关系如表所示:
下面用x表示y的式子中,正确的是( )
| x | 1 | 2 | 3 | 4 | … |
| y | 0.6+3 | 0.6+6 | 0.6+9 | 0.6+12 | … |
| A. | y=0.6+x | B. | y=0.6+3x | C. | y=0.6×3+x | D. | y=0.6×3-x |
5.小明所在的九年级一班共有38名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.67米,而小明的身高是1.66米,则下列说法错误的是( )
| A. | 1.67米是该班学生身高的平均水平 | |
| B. | 班上比小明矮的学生人数不会超过19人 | |
| C. | 这组身高数据的中位数不一定是1.67米 | |
| D. | 这组身高数据的众数不一定是1.67米 |
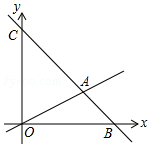 如图,在平面直角坐标系中,直线AB交x轴于点B(6,0),交y轴于点C(0,6),直线AB与直线OA:y=$\frac{1}{2}$x相交于点A,动点M在线段OA和射线AC上运动.
如图,在平面直角坐标系中,直线AB交x轴于点B(6,0),交y轴于点C(0,6),直线AB与直线OA:y=$\frac{1}{2}$x相交于点A,动点M在线段OA和射线AC上运动.