Question

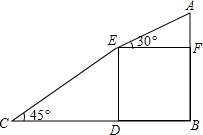一个人从山底爬到山顶，需先爬45°的山坡200米，再爬30°的山坡100米，求山高AB．

Answer 1

考点：解直角三角形的应用-坡度坡角问题

专题：

分析：分别利用锐角三角函数关系得出DE，AF的长，进而得出AB的长．

解答：解：由题意可得：
DE=ECsin45°=200×

2

2

=100

2

（m），
AF=AEsin30°=

1

2

AE=50（m），
故AB=AF+BF=（100

2

+50）m．
答：山高AB为（100

2

+50）m．

点评：此题主要考查了解直角三角形的应用，熟练掌握锐角三角函数关系是解题关键．