题目内容
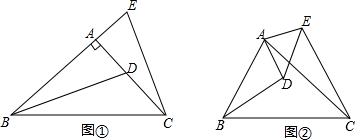
 在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足是Q,连接AP.
在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足是Q,连接AP.(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值.
考点:相似三角形的判定与性质,二次函数的最值
专题:
分析:(1)直接证明∠C=∠PQB=90°,而∠B=∠B,即可解决问题.
(2)设BP=λ,求出BQ、PQ、AQ的值(用λ表示),进而表示出△APQ的面积,借助二次函数的性质即可解决问题.
(2)设BP=λ,求出BQ、PQ、AQ的值(用λ表示),进而表示出△APQ的面积,借助二次函数的性质即可解决问题.
解答: 解:(1)∵PQ⊥AB,∠C=90°,
解:(1)∵PQ⊥AB,∠C=90°,
∴∠C=∠PQB=90°,
而∠B=∠B,
∴△PBQ∽△ABC.
(2)设△AQP面积的面积为α.
∵∠C=90°,AC=3,BC=4,
由勾股定理得:AB2=AC2+BC2
=9+16=25,
∴AB=5;设BP=λ,
∵△PBQ∽△ABC,
∴
=
=
,即
=
=
,
∴PQ=
,BQ=
,
∴AQ=5-
,
∴α=
AQ•PQ=
×
(5-
)
=-
λ2+
,
∴当λ=-
=
时,α取得最大值,
αmax=
=
.
即当BP=
时,△AQP面积最大,最大值=
.
 解:(1)∵PQ⊥AB,∠C=90°,
解:(1)∵PQ⊥AB,∠C=90°,∴∠C=∠PQB=90°,
而∠B=∠B,
∴△PBQ∽△ABC.
(2)设△AQP面积的面积为α.
∵∠C=90°,AC=3,BC=4,
由勾股定理得:AB2=AC2+BC2
=9+16=25,
∴AB=5;设BP=λ,
∵△PBQ∽△ABC,
∴
| PB |
| AB |
| PQ |
| AC |
| BQ |
| BC |
| λ |
| 5 |
| PQ |
| 3 |
| BQ |
| 4 |
∴PQ=
| 3λ |
| 5 |
| 4λ |
| 5 |
∴AQ=5-
| 4λ |
| 5 |
∴α=
| 1 |
| 2 |
| 1 |
| 2 |
| 3λ |
| 5 |
| 4λ |
| 5 |
=-
| 6 |
| 25 |
| 3λ |
| 2 |
∴当λ=-
| ||
2×(-
|
| 25 |
| 8 |
αmax=
-(
| ||
4×(-
|
| 75 |
| 32 |
即当BP=
| 25 |
| 8 |
| 75 |
| 32 |
点评:该题主要考查了相似三角形的判定及其性质、二次函数的性质及其性质的应用问题;解题的关键是灵活运用有关定理来分析、解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
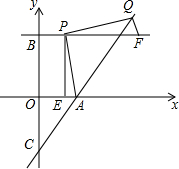 在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=Rt∠,直线AQ交y轴于点C
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=Rt∠,直线AQ交y轴于点C