题目内容
7.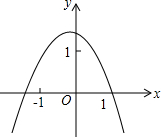 从如图所示的二次函数y=ax2+bx+c的图象中,孔明同学观察得出了下面四条信息:①b2-4ac>0;②c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )
从如图所示的二次函数y=ax2+bx+c的图象中,孔明同学观察得出了下面四条信息:①b2-4ac>0;②c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据抛物线与x轴的交点情况判断b2-4ac的符号;根据抛物线与y轴的交点判断c的大小;根据开口方向和对称轴,判断2a-b的符号;根据x=1时,y<0,判断a+b+c的符号.
解答 解:(1)根据图象,该函数图象与x轴有两个交点,
∴△=b2-4ac>0;
故(1)正确;
(2)由图象知,该函数图象与y轴的交点在点(0,1)的上方,
∴c>1;
故(2)正确;
(3)对称轴x=-$\frac{b}{2a}$>-1;
又∵函数图象的开口方向向下,
∴a<0,
∴-b<-2a,即2a-b<0,
故(3)正确;
(4)根据图示可知,当x=1时,即y=a+b+c<0,
故(4)错误.
故选:A.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列运算正确的是( )
| A. | $\sqrt{9}$=-3 | B. | |-3|=-3 | C. | -$\sqrt{-9}$=-3 | D. | -32=-9 |
12.下列函数中,自变量x的取值范围是x>-2的是( )
| A. | y=x+2 | B. | y=$\frac{1}{x+2}$ | C. | y=$\sqrt{x+2}$ | D. | y=$\frac{x-2}{\sqrt{x+2}}$ |
19.(1)计算:${-1}^{2008}+2sin45°+(\frac{1}{2})^{-1}$
(2)化简:$\frac{a-1}{a-2}÷\frac{{a}^{2}-2a+1}{2a-4}$.
(2)化简:$\frac{a-1}{a-2}÷\frac{{a}^{2}-2a+1}{2a-4}$.
16.已知反比例函数y=$\frac{10}{x}$,当1<x<2时,y的取值范围是( )
| A. | 0<x<5 | B. | 1<y<2 | C. | 5<y<10 | D. | y>10 |
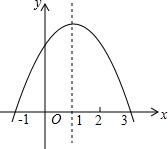 已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.
已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.