题目内容
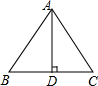如图，等腰△ABC中，AB=AC，AD是底边上的高，若AB=5cm，BC=6cm，则AD=（ ）cm．| A、4 | B、3 | C、2 | D、1 |
考点：等腰三角形的性质,勾股定理
专题：
分析：先根据等腰三角形的性质求出BD，再根据勾股定理求出AD．
解答：解：∵等腰△ABC中，AB=AC，AD是底边上的高，BC=6cm，
∴BD=CD=3cm，AD⊥BC，
在直角△ABD中，∵∠ADB=90°，AB=5cm，BD=3cm，
∴AD=
=4cm．
故选A．
∴BD=CD=3cm，AD⊥BC，
在直角△ABD中，∵∠ADB=90°，AB=5cm，BD=3cm，
∴AD=
| AB2-BD2 |
故选A．
点评：本题考查了等腰三角形三线合一的性质，勾股定理的应用，关键是求出BD的长．
练习册系列答案
名校课堂系列答案
相关题目
下列函数中，二次函数是（ ）
| A、y=2x-3 | ||
| B、y=x2-2 | ||
| C、y=（x-5）2-x2 | ||
D、y=
|
下面计算不正确的是（ ）
| A、x5+x5=2x5 | ||
| B、（-x）3•（-x）5=-x8 | ||
| C、x3•（-x5）2=x13 | ||
D、（-2xy）3•
|
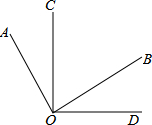如图，∠AOB，∠COD都是直角，下列结论：①∠AOC=∠BOD；②∠AOC+∠BOD=90°；③若OC平分∠AOB，则OB平分∠COD；④∠AOD的平分线与∠COB的平分线是同一条射线．其中正确的个数有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
已知等腰三角形的一边等于8cm，另一边等于6cm，则此三角形的周长是（ ）cm．
| A、22 | B、20 |
| C、22或20 | D、无法确定 |
如图，l是线段AB的对称轴，l′是线段BC的对称轴，l和l′相交于点O．OA与OC相等吗？为什么？