题目内容
18.抛物线y=-x2+3x+4与x轴交点为A、B,顶点为C,则△ABC的面积是$\frac{125}{8}$.分析 先根据抛物线与x轴的交点求出A点和B点坐标,再利用配方法得到抛物线的顶点C的坐标,然后根据三角形面积公式求解.
解答 解:当y=0时,-x2+3x+4=0,解得x1=4,x2=-1,则A(4,0),B(-1,0),所以AB=4-(-1)=5,
当y=0时,y=-x2+3x+4=-(x-$\frac{3}{2}$)2+$\frac{25}{4}$,则C($\frac{3}{2}$,$\frac{25}{4}$),
所以△ABC的面积=$\frac{1}{2}$×5×$\frac{25}{4}$=$\frac{125}{8}$.
故答案为$\frac{125}{8}$.
点评 本题考查了抛物线与x轴的交点:利用二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0),且这两个交点为抛物线上的对称点.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
10.生括中的“对称美”比比皆是,人们把闹钟和飞机制造成对称形状,不仅为了美观,而且还有一定的科学道理:闹钟的对称保证了指针走时的均匀性,飞机的对称能使飞机在空中飞行时保持平衡.下列说法正确的是( )
| A. | 三叶电扇是轴对称图形 | B. | 飞机的两个翅膀是全等形 | ||
| C. | 三角形是轴对称图形 | D. | 圆不是轴对称图形 |
7.某商场对上周女装的销售情况进行了统计,如下表:
经理决定本周进女装时多进L号,可用来解释这一现象的统计量是( )
| 尺寸 | S | M | L | XL | XXL |
| 数量(件) | 50 | 110 | 150 | 80 | 70 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
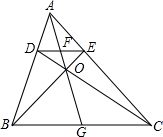 如图所示,已知在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于O,AO和DE相交于F,AO的延长线和BC交于G,证明:
如图所示,已知在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于O,AO和DE相交于F,AO的延长线和BC交于G,证明: 如图,正方形ABCD的边长为3,点E在边AB上,AE=1,点Q是边AD上的动点,过点Q作QH⊥BC于H,在BC上H点左侧取点P,使得PH=1,若设BP=x,EQ2=y.
如图,正方形ABCD的边长为3,点E在边AB上,AE=1,点Q是边AD上的动点,过点Q作QH⊥BC于H,在BC上H点左侧取点P,使得PH=1,若设BP=x,EQ2=y.