题目内容
以下列线段为边能组成三角形的是( )
| A、8cm,6cm,4cm |
| B、12cm,5cm,6cm |
| C、3cm,3cm,6cm |
| D、1cm,2cm,4cm |
考点:三角形三边关系
专题:
分析:根据三角形三边关系定理:三角形两边之和大于第三边进行解答.
解答:解:A、4+6>8,能组成三角形,故此选项正确;
B、5+6=11<12,不能组成三角形,故此选项错误;
C、3+3=6,不能组成三角形,故此选项错误;
D、1+2<4,不能组成三角形,故此选项错误;
故选:A.
B、5+6=11<12,不能组成三角形,故此选项错误;
C、3+3=6,不能组成三角形,故此选项错误;
D、1+2<4,不能组成三角形,故此选项错误;
故选:A.
点评:此题主要考查了三角形的三边关系,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列判断正确的是( )
A、
| ||
| B、解方程-x-x=2,得x=1 | ||
C、方程
| ||
| D、从9+x=4x-2得x+4x=9-2 |
已知关于x的一元二次方程x2-3x+2=0两实数根为x1、x2,则x1+x2=( )
| A、3 | B、-3 | C、1 | D、-1 |
关于x的一元二次方程x2-(2m-1)x+m+3=0的两根为x1,x2,且满足x1x2-x1-x2=1,则m的值为( )
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
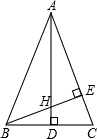 如图,△ABC中,AB=AC,AD⊥BC,BE⊥AC,AD和BE交于点H,且AE=BE,求证:AH=2BD.
如图,△ABC中,AB=AC,AD⊥BC,BE⊥AC,AD和BE交于点H,且AE=BE,求证:AH=2BD.