题目内容
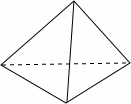
图1中的中国结挂件是由四个相同的菱形在顶点处依 次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.
次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.
(1)连接CD,EB,猜想它们的位置关系并加以证明;
(2)求A,B两点之间的距离(结果取整数,可以使用计算器)
(参考数据: ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.45)
≈2.45)

解:(1)猜想CD∥EB.
证明:连接DE.
∵中国结挂件是四个相同的菱形,每相邻两个菱形均成30°的夹角,菱形的锐角为60°
∴∠CDE=60°÷2×2+30°=90°,
∴∠BED=60°÷2×2+30°=90°,
∴∠CDE=∠BED,
∴CD∥EB.
(2)BE=2OE=2×10×cos30°=10 cm,
cm,
同理可得, DE=10
DE=10 cm,
cm,
则BD=10 cm,
cm,
同理可得,AD=10 cm,
cm,
AB=BD+AD=20 ≈49cm.
≈49cm.
答:A,B两点之间的距离大约为49cm.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案实数2的倒数是( )
|
| A. | ﹣ | B. | ± | C. | 2 | D. |
|
为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答问题:
| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5~60.5 | 16 | 0.08 |
| 二 | 60.5~70.5 | 30 | 0.15 |
| 三 | 70.5~80.5 | 50 | 0.25 |
| 四 | 80.5~90.5 | m | 0.40 |
| 五 | 90.5~24 | n |
(1)本次抽样调查的样本容量为 200 ,此样本中成绩的中位数落在第 四 组内,表中m= 80 ,n= ;
(2)补全频数分布直方图;
(3)若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?

如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

|
| A. | 4,30° | B. | 2,60° | C. | 1,30° | D. | 3,60° |
大庆油田某一年的石油总产量为4 500万吨,若用科学记数法表示应为( )吨.
|
| A. | 4.5×10﹣6 | B. | 4.5×106 | C. | 4.5×107 | D. | 4.5×108 |

 ﹣
﹣ )÷
)÷ .
.