题目内容
 如图所示,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,DC=5,则AB=
如图所示,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,DC=5,则AB=考点:角平分线的性质,勾股定理
专题:
分析:过D作DE⊥BC,根据角平分线的性质可得DE=AD=3,再根据勾股定理可得EC=5,然后再证明Rt△ABD≌Rt△EBD,可得AB=EB,再利用勾股定理计算出AB的长即可.
解答: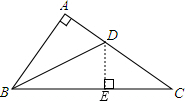 解:过D作DE⊥BC,
解:过D作DE⊥BC,
∵∠ABC的平分线BD交AC于点D,
∴DE=AD=3,
∵DC=5,
∴EC=
=4,
在Rt△ABD和Rt△EBD中,
,
∴Rt△ABD≌Rt△EBD(HL),
∴AB=EB,
设AB=x,则CB=x+4,
x2+82=(x+4)2,
解得:x=6,
故答案为:6.
 解:过D作DE⊥BC,
解:过D作DE⊥BC,∵∠ABC的平分线BD交AC于点D,
∴DE=AD=3,
∵DC=5,
∴EC=
| 52-32 |
在Rt△ABD和Rt△EBD中,
|
∴Rt△ABD≌Rt△EBD(HL),
∴AB=EB,
设AB=x,则CB=x+4,
x2+82=(x+4)2,
解得:x=6,
故答案为:6.
点评:此题主要考查了角平分线的性质和勾股定理的应用,关键是掌握角平分线上的点到角两边的距离相等.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
根据下表的对应值,试判断一元二次方程ax2+bx+c=0的一解的取值范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.07 |
| A、3<x<3.23 |
| B、3.23<x<3.24 |
| C、3.24<x<3.25 |
| D、3.25<x<3.26 |
若函数y=(k-1)x+k2-1是正比例函数,则k的值是( )
| A、-1 | B、1 |
| C、-1或1 | D、任意实数 |
下列各式:
,
(a≥2),
,
,-
,其中二次根式有( )个.
| x2+1 |
| a-2 |
| (x-1)2 |
| -3 |
| x2+1 |
| A、3个 | B、4个 | C、5个 | D、6个 |
如果三个有理数的积是负数,那么这三个有理数中( )
| A、只有一个负数 |
| B、有两个负数 |
| C、三个都是负数 |
| D、有一个或三个负数 |
 如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.
如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.