题目内容
已知：关于
的一元二次方程
．
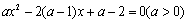（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为
，
（其中＞）．若
是关于
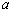的函数，且
，求这个函数的表达式；
（3）在（2）的条件下，结合函数的图象回答：若使
，则自变量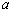的取值范围为 ．
（1）证明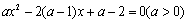：是关于的一元二次方程，
···················· 1分
=4．
即
．
方程有两个不相等的实数根．·················· 2分
（2） 解：由求根公式，得
．
∴
或
．······················· 3分
，＞，
，
．······················· 4分
．
即
为所求．………………………………………………………5分
（3）0＜≤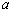
． …………………………………………………………………………7分
练习册系列答案
相关题目
，则∠BCE的度数是 .
某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按120个工时计算）生产空调、冰箱、彩电共360台，且彩电至少生产60台，已知生产这些家电产品每台所需工时和每台产值如下表：
| 家电名称 | 空调 | 冰箱 | 彩电 |
| 工时 |
|
|
|
| 产值（千元） | 4 | 3 | 2 |
问每周应生产空调、冰箱、彩电各多少台，才能使产值最高？最高产值是多少？
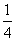
可得到△ABC≌△ABD，那么这个条件可以是 (要求：不在图中添加其他辅助线，写出一个条件即可 )．
的值为0，则
的值为
．
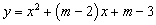总过x轴上的
与
的和仍是单项式，则
的值为____________．