Question

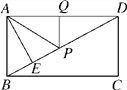
【题目】如图，在矩形ABCD中，AD＝6，AE⊥BD，垂足为E，DE＝3BE，点P，Q分别在BD，AD 上，则AP＋PQ的最小值为：

A. 2 B. C. 2 D. 3

Answer 1

【答案】D

【解析】试题解析：设BE=x，则DE=3x，∵四边形ABCD为矩形，且AE⊥BD，∴△ABE∽△DAE，∴=BEDE，即，∴AE=x，在Rt△ADE中，由勾股定理可得，即，解得x=，∴AE=3，DE=，

如图，设A点关于BD的对称点为A′，连接A′D，PA′，则A′A=2AE=6=AD，AD=A′D=6，

∴△AA′D是等边三角形，∵PA=PA′，∴当A′、P、Q三点在一条线上时，A′P+PQ最小，又垂线段最短可知当PQ⊥AD时，A′P+PQ最小，∴AP+PQ=A′P+PQ=A′Q=DE=，故选D．