题目内容
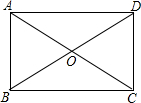已知：如图，在平行四边形ABCD中，AC交BD于点O，AC=8cm，∠AOB=60°．若AC=BD，试求平行四边形ABCD的面积．
解：∵AC=BD，四边形ABCD是平行四边形，
∴四边形ABCD是矩形．
∵AC=BD，
∴AO=BO，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴AB=BO=
=4，
∴BC=
=4
．
∴四边形ABCD的面积为：4×4=16．
分析：对角线相等的平行四边形是矩形，求出矩形的边长，可求出矩形的面积．
点评：本题考查矩形的性质定理和判定定理，判定是矩形后，从而可求出面积．
∴四边形ABCD是矩形．
∵AC=BD，
∴AO=BO，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴AB=BO=
=4，∴BC=
=4．∴四边形ABCD的面积为：4
×4=16．分析：对角线相等的平行四边形是矩形，求出矩形的边长，可求出矩形的面积．
点评：本题考查矩形的性质定理和判定定理，判定是矩形后，从而可求出面积．
练习册系列答案
阅读快车系列答案
相关题目
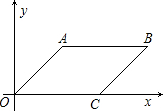如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，