题目内容
12.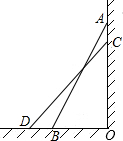 如图,梯子AB靠在墙上,梯子的顶端A到墙根O的距离为24m,梯子的底端B到地面的距离为7m,一不小心梯子顶端A下滑了4米到C,底端B滑动到D,那么BD的长是( )
如图,梯子AB靠在墙上,梯子的顶端A到墙根O的距离为24m,梯子的底端B到地面的距离为7m,一不小心梯子顶端A下滑了4米到C,底端B滑动到D,那么BD的长是( )| A. | 2m | B. | 4m | C. | 6m | D. | 8m |
分析 由题意可知OB=7m,OA=24m,先利用勾股定理求出AB,梯子移动过程中长短不变,所以AB=DC,又由题意可知OD=15m,进而得出答案.
解答 解:在直角三角形AOB中,因为AO=24m,OB=7m,
由勾股定理得:AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=25(m),
由题意可知AB=CD,
又OC=24-4=20(m),根据勾股定理得:OD=$\sqrt{D{C}^{2}-C{O}^{2}}$=15(m),
故BD=DO-BO=15-7=8(米).
故选:D.
点评 本题考查了勾股定理的应用,解题时注意勾股定理应用的环境是在直角三角形中.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
3.小明家使用的电冰箱冷藏室的温度是4℃,冷冻室比冷藏室的温度低18℃,则冷冻室的温度是( )
| A. | -14℃ | B. | 14℃ | C. | 22℃ | D. | -22℃ |
7. 如图,在△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,下列结论中一定成立的是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,下列结论中一定成立的是( )
 如图,在△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,下列结论中一定成立的是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,下列结论中一定成立的是( )| A. | ∠ABE=∠DFE | B. | AE=ED | C. | AD=DC | D. | AB=BF |
2.已知x=1是一元二次方程(m+1)x2-m2x-2m-1=0的一个实数根,则m的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 0或-1 |
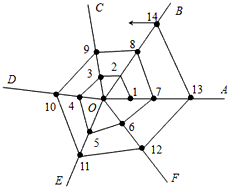 右图是蜘蛛结网过程示意图,一只蜘蛛先以O为起点结六条线OA,OB,OC,OD,OE,OF后,再从线OA上某点开始按逆时针方向依次在OA,BO,OC,OD,OE,OF,OA,OB,OF,OA,OB…上结网,若将各线上的结点依次记为1、2、3、4、5、6、7、8、…,那么第200个结点在OB条线段上.
右图是蜘蛛结网过程示意图,一只蜘蛛先以O为起点结六条线OA,OB,OC,OD,OE,OF后,再从线OA上某点开始按逆时针方向依次在OA,BO,OC,OD,OE,OF,OA,OB,OF,OA,OB…上结网,若将各线上的结点依次记为1、2、3、4、5、6、7、8、…,那么第200个结点在OB条线段上.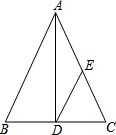 如图,已知在△ABC中,AB=AC,AD是BC边上的高线,DE∥AB交AC于点E,猜想DE与AB的数量关系,并证明你的猜想.
如图,已知在△ABC中,AB=AC,AD是BC边上的高线,DE∥AB交AC于点E,猜想DE与AB的数量关系,并证明你的猜想.