题目内容
5. 如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.
如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.(1)试判断四边形DEFG的形状,并说明理由;
(2)填空:
①若AB=3,当CA=CB时,四边形DEFG的面积是$\frac{3}{2}$;
②若AB=2,当∠CAB的度数为75°或15°时,四边形DEFG是正方形.
分析 (1)只要证明DG=EF,DG∥EF即可解决问题;
(2)①只要证明四边形DEFG是矩形即可解决问题;
②分点C在优弧AB或劣弧AB上两种切线讨论即可;
解答 解:(1)四边形DEFG是平行四边形.
∵点D、E、F、G分别是CA、OA、OB、CB的中点,
∴DG∥AB,DG=$\frac{1}{2}$AB,EF∥AB,EF=$\frac{1}{2}$AB,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)①连接OC.
∵CA=CB,
∴$\widehat{AC}$=$\widehat{BC}$,
∴DG⊥OC,
∵AD=DC,AE=EO,
∴DE∥OC,DE=$\frac{1}{2}$OC=1,同理EF=$\frac{1}{2}$AB=$\frac{3}{2}$,
∴DE⊥DG,
∴四边形DEFG是矩形,
∴四边形DEFG的面积=$\frac{3}{2}$.
故答案为$\frac{3}{2}$;
②当C是优弧AB的中点时,四边形DEFG是正方形,此时∠CAB=75°,
当C是劣弧AB的中点时,四边形DEFG是正方形,此时∠CAB=15°,
故答案为75°或15°.
点评 本题考查的是三角形的外接圆、正方形的性质和判定、三角形的中位线定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
14.下表是全国7个城市2017年3月份某日空气质量指数(AQI)的统计结果:
该日空气质量指数的中位数是( )
| 城市 | 北京 | 成都 | 深圳 | 长沙 | 上海 | 武汉 | 广州 |
| AQI指数 | 25 | 72 | 49 | 241 | 62 | 185 | 49 |
| A. | 49 | B. | 62 | C. | 241 | D. | 97 |
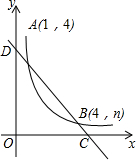 如图,直线y1=ax+b与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,4)、B(4,n)两点,与x轴、y轴交于C、D两点.
如图,直线y1=ax+b与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,4)、B(4,n)两点,与x轴、y轴交于C、D两点.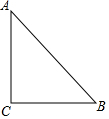 如图,Rt△ABC中,∠C=90°,AC=BC=5,若P为平面内一点,且AP=$\sqrt{10}$,BP=2$\sqrt{5}$,则CP=5或$\sqrt{5}$.
如图,Rt△ABC中,∠C=90°,AC=BC=5,若P为平面内一点,且AP=$\sqrt{10}$,BP=2$\sqrt{5}$,则CP=5或$\sqrt{5}$.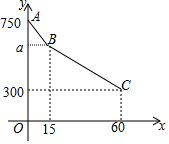 周末,小军在医院里照顾奶奶输液,小军问:“按照这样的输液速度,多少时间能结束输液?”护上答:“75分钟.”15分钟后,小军减慢了输液的速度,60分钟后,小军发现还剩有300毫升药液,剩下待输药液y(毫升)与输液时间x(分钟)的函数关系如图所示.
周末,小军在医院里照顾奶奶输液,小军问:“按照这样的输液速度,多少时间能结束输液?”护上答:“75分钟.”15分钟后,小军减慢了输液的速度,60分钟后,小军发现还剩有300毫升药液,剩下待输药液y(毫升)与输液时间x(分钟)的函数关系如图所示.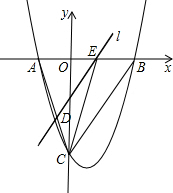 如图,抛物线y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4与x轴交于A,B两点,与y轴交于点C,连接BC,AC.
如图,抛物线y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4与x轴交于A,B两点,与y轴交于点C,连接BC,AC.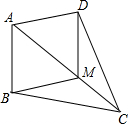 在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.
在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.