题目内容
15.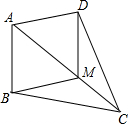 在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.
在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.
分析 只要证明AB=BM=MD=DA,即可解决问题.
解答 证明: ∵AB∥DM,
∵AB∥DM,
∴∠BAM=∠AMD,
∵△ADC是由△ABC翻折得到,
∴∠CAB=∠CAD,AB=AD,BM=DM,
∴∠DAM=∠AMD,
∴DA=DM=AB=BM,
∴四边形ABMD是菱形.
点评 本题考查翻折变换、等腰三角形的判定和性质.平行线的性质等知识,解题的关键是证明△ADM是等腰三角形.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
3.在平面直角坐标系中,点(3,-2)关于原点对称的点是( )
| A. | (-3,2) | B. | (-3,-2) | C. | (3,-2) | D. | (3,2) |
7.盒中有x枚黑色棋子和y枚白色棋子,这些棋子除颜色外无其他差别.若从盒中随机取出一枚棋子,则它是黑色棋子的概率是$\frac{3}{8}$;若往盒中再放进10枚黑色棋子,则取得黑色棋子的概率变为$\frac{1}{2}$,则x+y的值是( )
| A. | 38 | B. | 40 | C. | 42 | D. | 30 |
4.2017年5月14日首届“一带一路”国际高峰论坛在中国北京召开,来自130多个国家的约1 500名各界贵宾出席论坛.用科学记数法表示1 500是( )
| A. | 15×102 | B. | 1.5×102 | C. | 1.5×103 | D. | 0.15×104 |
5.-2017的绝对值是( )
| A. | -2017 | B. | -$\frac{1}{2017}$ | C. | 2017 | D. | $\frac{1}{2017}$ |
 如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.
如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.