题目内容
9.已知c的立方根为3,且(a-4)2+$\sqrt{b-3}$=0,则a+6b+c的平方根是±7.分析 先依据立方根的定义、非负数的性质求得a、b、c的值,然后再求得代数式的值,最后利用平方根的性质求解即可.
解答 解:∵c的立方根为3,且(a-4)2+$\sqrt{b-3}$=0,
∴c=27,a=4,b=3.
∴a+6b+c=4+18+27=49.
49的平方根是±7.
故答案为:±7.
点评 本题主要考查的是立方根的定义、平方根的定义,非负数的性质,求得a、b、c的值是解题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
17.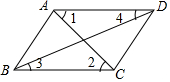 如图,下列条件中不能判定AD∥BC的是( )
如图,下列条件中不能判定AD∥BC的是( )
 如图,下列条件中不能判定AD∥BC的是( )
如图,下列条件中不能判定AD∥BC的是( )| A. | ∠BAD+∠ABC=180° | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠BAD=∠BCD |
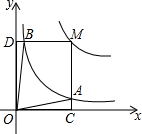 反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.
反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.