Question

14．如图，Rt△ABC中，∠ACB=90°，AC=BC，点D在斜边AB上，且AD=AC，过点B作BE⊥CD交直线CD于点E．
（1）求∠BCD的度数；
（2）求证：CD=2BE．

Answer 1

分析 （1）根据等腰直角三角形的性质得到∠A=∠B=45°，根据等腰三角形的性质计算即可；
（2）作AF⊥CD，证明△AFD≌△CEB，根据全等三角形的性质证明即可．

解答 解：（1）∵∠ACB=90°，AC=BC，
∴∠A=∠B=45°，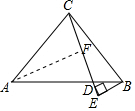
∵AD=AC，
∴∠ACD=∠ADC=$\frac{180°-45°}{2}$=67.5°，
∴∠BCD=90°-67.5°=22.5°；
（2）证明：作AF⊥CD，
∵AD=AC，
∴CF=FD=$\frac{1}{2}$CD，∠FAD=$\frac{1}{2}∠$CAB=22.5°，
∵∠ADC=67.5°，
∴∠BDE=67.5°，
∴∠DBE=22.5°，
∴∠CBE=67.5°，
在△AFD和△CEB中，
$\left\{\begin{array}{l}{∠AFD=∠CEB}\\{∠ADF=∠CBE}\\{AD=CB}\end{array}\right.$，
∴△AFD≌△CEB，
∴BE=DF，
∴CD=2BE．

点评 本题考查的是全等三角形的判定和性质、等腰直角三角形的性质，掌握三角形全等的判定定理和性质定理是解题的关键．