题目内容
如图,△ABC是直角三角形,∠BAC=90°,AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm.
(1)求AD的长;
(2)求△AEC的面积.
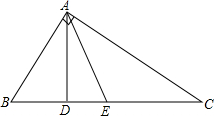
(1)求AD的长;
(2)求△AEC的面积.

∵∠BAC=90°,AD是边BC上的高,
∴
AB•AC=
BC•AD,
∴AD=
=
=4.8(cm),即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=
AB•AC=
×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴
BE•AD=
EC•AD,即S△ABE=S△AEC,
∴S△AEC=
S△ABC=12(cm2).
∴△AEC的面积是12cm2.
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AB•AC |
| BC |
| 6×8 |
| 10 |
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AE是边BC的中线,
∴BE=EC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AEC=
| 1 |
| 2 |
∴△AEC的面积是12cm2.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目