题目内容
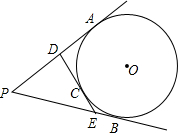
 如图,从⊙O外一点P引圆的两条切线PA、PB,切点为A、B,点C是劣弧AB上一点,过C的切线交PA、PB分别于M、N,若⊙O的半径为2,∠P=60°,则△PMN的周长为
如图,从⊙O外一点P引圆的两条切线PA、PB,切点为A、B,点C是劣弧AB上一点,过C的切线交PA、PB分别于M、N,若⊙O的半径为2,∠P=60°,则△PMN的周长为
- A.4
- B.6
- C.

- D.

C
分析:连接OP,由圆外一点P作圆的两条切线PA与PB,根据切线长定理得到PA=PB,且PO为角平分线,由∠APB=60°,得到∠APO=30°,再由切线的性质得到OA与AP垂直,在直角三角形APO中,根据30°角所对的直角边等于斜边的一半,由半径OA的长求出斜边OP的长,再利用勾股定理求出AP的长,由MA与MC为圆O的切线,根据切线长定理得到MA=MC,同理可得NB=NC,然后把三角形PMN的三边相加表示出三角形PMN的周长,等量代换后得到其周长为2PA,把PA的长代入即可求出三角形PMN的周长.
解答:连接OP,

∵PA,PB为圆O的切线,
∴PA=PB,PO平分∠APB,OA⊥AP,
又∠APB=60°,
∴∠APO=30°,
在直角三角形APO中,OA=2,
∴OP=2OA=4,
根据勾股定理得:PA= =2
=2 ,
,
∵MA,MC为圆O的两条切线,
∴MA=MC,
又NB,NC为圆O的切线,
∴NC=NB,
∴△PMN的周长=PM+PN+MN
=PM+PN+MC+NC
=PM+PN+MA+NB
=PA+PB=2PA
=4 .
.
故选C
点评:此题考查了切线长定理,切线的性质,勾股定理,含30°角直角三角形的性质,利用了转化的思想,熟练掌握切线长定理是解本题的关键.
分析:连接OP,由圆外一点P作圆的两条切线PA与PB,根据切线长定理得到PA=PB,且PO为角平分线,由∠APB=60°,得到∠APO=30°,再由切线的性质得到OA与AP垂直,在直角三角形APO中,根据30°角所对的直角边等于斜边的一半,由半径OA的长求出斜边OP的长,再利用勾股定理求出AP的长,由MA与MC为圆O的切线,根据切线长定理得到MA=MC,同理可得NB=NC,然后把三角形PMN的三边相加表示出三角形PMN的周长,等量代换后得到其周长为2PA,把PA的长代入即可求出三角形PMN的周长.
解答:连接OP,

∵PA,PB为圆O的切线,
∴PA=PB,PO平分∠APB,OA⊥AP,
又∠APB=60°,
∴∠APO=30°,
在直角三角形APO中,OA=2,
∴OP=2OA=4,
根据勾股定理得:PA=
 =2
=2 ,
,∵MA,MC为圆O的两条切线,
∴MA=MC,
又NB,NC为圆O的切线,
∴NC=NB,
∴△PMN的周长=PM+PN+MN
=PM+PN+MC+NC
=PM+PN+MA+NB
=PA+PB=2PA
=4
 .
.故选C
点评:此题考查了切线长定理,切线的性质,勾股定理,含30°角直角三角形的性质,利用了转化的思想,熟练掌握切线长定理是解本题的关键.

练习册系列答案
相关题目
 如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,若PA=8cm,C是
如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,若PA=8cm,C是
 如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O直径BD=6,连接CD、AO.
如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O直径BD=6,连接CD、AO. 20、如图,从圆外一点P引圆的切线PA,点A为切点,割线PDB交⊙O于点D、B.已知PA=12,PD=8,则S△ABP:S△DAP=
20、如图,从圆外一点P引圆的切线PA,点A为切点,割线PDB交⊙O于点D、B.已知PA=12,PD=8,则S△ABP:S△DAP= 17、如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=26°,则∠ACB的度数为
17、如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=26°,则∠ACB的度数为 如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,若PA=5cm,C是
如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,若PA=5cm,C是