题目内容
17、如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC．若∠A=26°，则∠ACB的度数为32°
．分析：连接OB，根据切线的性质，得∠OBA=90°，又∠A=26°，所以∠AOB=64°，再用三角形的外角性质可以求出∠ACB的度数．
解答：
解：如图：连接OB，
∵AB切⊙O于点B，
∴∠OBA=90°，
∵∠A=26°，
∴∠AOB=90°-26°=64°，
∵OB=OC，
∴∠C=∠OBC，
∵∠AOB=∠C+∠OBC=2∠C，
∴∠C=32°．
故答案是：32°．
解：如图：连接OB，∵AB切⊙O于点B，
∴∠OBA=90°，
∵∠A=26°，
∴∠AOB=90°-26°=64°，
∵OB=OC，
∴∠C=∠OBC，
∵∠AOB=∠C+∠OBC=2∠C，
∴∠C=32°．
故答案是：32°．
点评：本题考查的是切线的性质，利用切线的性质，结合三角形内角和求出角的度数．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
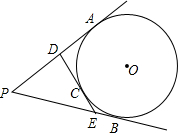如图，从⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，若PA=8cm，C是
如图，从⊙O外一点A作⊙O的切线AB、AC，切点分别为B、C，且⊙O直径BD=6，连接CD、AO．
20、如图，从圆外一点P引圆的切线PA，点A为切点，割线PDB交⊙O于点D、B．已知PA=12，PD=8，则S△ABP：S△DAP=
如图，从⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，若PA=5cm，C是