Question

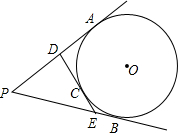
如图，从⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，若PA=5cm，C是

AB

上的一个动点（点C与A、B两点不重合），过点C作⊙O的切线，分别交PA、PB于点D、E，求△PED的周长是多少？

Answer 1

分析：根据切线长定理求出AP=BP，DA=DC，CE=BE，代入求出△PDE的周长为2PA，代入即可．

解答：解：∵PA、PB、DE是圆O的切线，切点分别是A、B、C，
∴AP=BP，DA=DC，CE=BE，
∴△PED的周长是：PD+DE+PE
=PD+DC+CE+PE
=PD+DA+PE+BE
=PA+PB
=2PA=10cm．
答：△PED的周长是10cm．

点评：本题考查了切线长定理的应用，解此题的关键是求出AP=BP，DA=DC，CE=BE，把△PDE的周长转化成含有PA的式子，题型较好，难度适中．