题目内容
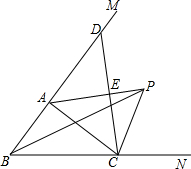如图，在△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点P，连接AP．（1）求证：PA平分∠BAC的外角∠CAM；
（2）过点C作CE⊥AP，E是垂足，并延长CE交BM于点D．求证：CE=ED．
考点：角平分线的性质,等腰三角形的判定与性质
专题：证明题
分析：（1）过P作PT⊥BC于T，PS⊥AC于S，PQ⊥BA于Q，根据角平分线性质求出PQ=PS=PT，根据角平分线性质得出即可；
（2）根据ASA求出△AED≌△AEC即可．
（2）根据ASA求出△AED≌△AEC即可．
解答：证明：（1）
过P作PT⊥BC于T，PS⊥AC于S，PQ⊥BA于Q，如图，
∵在△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点P，
∴PQ=PT，PS=PT，
∴PQ=PS，
∴AP平分∠DAC，
即PA平分∠BAC的外角∠CAM；
（2）∵PA平分∠BAC的外角∠CAM，
∴∠DAE=∠CAE，
∵CE⊥AP，
∴∠AED=∠AEC=90°，
在△AED和△AEC中
∴△AED≌△AEC，
∴CE=ED．
过P作PT⊥BC于T，PS⊥AC于S，PQ⊥BA于Q，如图，
∵在△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点P，
∴PQ=PT，PS=PT，
∴PQ=PS，
∴AP平分∠DAC，
即PA平分∠BAC的外角∠CAM；
（2）∵PA平分∠BAC的外角∠CAM，
∴∠DAE=∠CAE，
∵CE⊥AP，
∴∠AED=∠AEC=90°，
在△AED和△AEC中
|
∴△AED≌△AEC，
∴CE=ED．
点评：本题考查了角平分线性质和全等三角形的性质和判定的应用，解此题的关键是能正确作出辅助线并进一步求出PQ=PS和△AED≌△AEC，注意：角平分线上的点到角两边的距离相等．
练习册系列答案
相关题目
如图，两个相同的可以自由转动的转盘A和B，A盘被平均分为12份，颜色顺次为红，绿，蓝；B盘被平均分为红，绿和蓝3份，分别转动A盘和B盘，A盘停止时指针指向红色的概率与B盘停止时指针指向红色的概率哪个大？为什么？如果几个最简二次根式的被开方数相同，那么这几个最简二次根式叫做同类二次根式．下列各组根式中，最同类二次根式的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列计算正确的是（ ）
| A、x2+x3=x5 |
| B、x2•x3=x5 |
| C、（x2）3=x5 |
| D、x6÷x2=x3 |