已知:如图.A.B.C.D四点对应的实数都是整数.若点A对应于实数a.点B对应于实数b.点C对应于实数c.数轴上每个小格对应一个单位长度且c-2b=5.那么数轴上的原点应是( )点．A．A点B．B点C．C点D．D点题目和参考答案——青夏教育精英家教网—

题目内容

10．

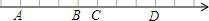已知：如图，A，B，C，D四点对应的实数都是整数，若点A对应于实数a，点B对应于实数b，点C对应于实数c，数轴上每个小格对应一个单位长度且c-2b=5，那么数轴上的原点应是（　　）点．

A．

A点

B．

B点

C．

C点

D．

D点

分析根据实数与数轴的关系得到c-b=1，c-2b=5建立方程组，解得b=-4，c=-3，即可确定原点．

解答解：由数轴可得，c-b=1①，
∵c-2b=5②，
解由①②所组成的方程组得，b=-4，c=-3，
∴数轴上的原点应是D点．
故选：D．

点评本题考查了实数与数轴的关系：实数与数轴上的点是一一对应的关系；原点左边的点对应负实数，右边的点对应正实数；离原点越远，其点对应的实数的绝对值越大．

练习册系列答案

名校学案名校小状元系列答案

	A．	$\sqrt{（-4）×（-25）}$=$\sqrt{-4}$×$\sqrt{-25}$=10		B．	$\sqrt{{2^2}+{3^2}}$=2+3=5
	C．	$\sqrt{\frac{2}{3}}$=$\frac{1}{3}$$\sqrt{6}$		D．	$\frac{{-\sqrt{45}}}{{\sqrt{5}}}=\sqrt{\frac{-45}{5}}$

试题分类