题目内容
如图①,梯形ABCD中,DC∥AB,DE⊥AB于点E.
阅读理解:
在图①中,延长梯形ABCD的两腰AD、BC交于点P,过点D作DF∥CB交AB于点F,得到图②;四边形BCDF的面积为![]() ,△ADF的面积
,△ADF的面积![]() ,△PDC的面积
,△PDC的面积![]() .
.

1.在图②中,若DC=2,AB=8,DE=3,则![]() ,
,![]() ______,
______,![]() ;
;
2.在图②中,若![]() ,
,![]() ,
,![]() ,则
,则![]() =__________,并写出理由;
=__________,并写出理由;
3.如图③,□DEFC的四个顶点在△PAB的三边上,若△PDC、△ADE、△CFB的面积分别为2、3、5,试利用(2)中的结论求△PAB的面积.

1.![]() ,
,![]() 9,
9,![]() 1…………………………3分
1…………………………3分
2.4……………………………………………………4分
理由:∵DF∥CB,DC∥AB,
∴四边形BCDF为平行四边形,![]() ,
,![]() .
.
∴△PDC∽△ADF,BF=DC=b,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]()
∵![]() ,∴
,∴![]() =4………………………………………………7分
=4………………………………………………7分
3.解:过点D作DH∥PB交AB于H,则四边形BCDH为平行四边形.

∴![]() ,
,![]() ,
,![]() .
.
∵四边形DEFC为平行四边形,
∴![]() . ∴
. ∴![]() .
.
∴![]() . ∴△DBF≌△HDE.
. ∴△DBF≌△HDE.
∴△ADH的面积为![]() .
.
由(2)得,□BCDH的面积为![]() .
.
∴△ABC的面积为![]() .……………………10分
.……………………10分
(说明:未利用(2)中的结论,但正确地求出了△ABC的面积,给2分)
解析:略

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数. 如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?
如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形? 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=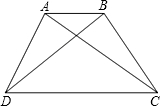 如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积.
如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积. 如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=
如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=