题目内容
9. 如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是$\sqrt{2}+\sqrt{6}$.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是$\sqrt{2}+\sqrt{6}$.
分析 首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在根据勾股定理求解.
解答 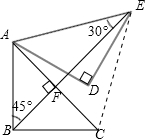 解:连结CE,设BE与AC相交于点F,如下图所示,
解:连结CE,设BE与AC相交于点F,如下图所示,
∵Rt△ABC中,AB=BC,∠ABC=90°,
∴∠BCA=∠BAC=45°,
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,
∴∠BAC=∠DAE=45°,AC=AE,
又∵旋转角为60°,
∴∠BAD=∠CAE=60°,
∴△ACE是等边三角形
∴AC=CE=AE=2$\sqrt{2}$,
在△ABE与△CBE中,$\left\{\begin{array}{l}{BA=BC}\\{AE=CE}\\{BE=BE}\end{array}\right.$,
∴△ABE≌△CBE,
∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°,
∴在△ABF中,∠BFA=180°-45°-45°=90°,
∴∠AFB=∠AFE=90°,
在Rt△ABF中,由勾股定理得,
BF=AF=$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$,
又在Rt△AFE中,∠AEF=30°,∠AFE=90°,
∴FE=$\sqrt{3}$AF=$\sqrt{6}$
∴BE=BF+FE=$\sqrt{2}$+$\sqrt{6}$,
故答案为:$\sqrt{2}+\sqrt{6}$.
点评 此题是旋转性质题,解决此题,关键是思路要明确:“构造”直角三角形.在熟练掌握旋转的性质的基础上,还要应用全等的判定及性质,直角三角形的判定及勾股定理的应用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
19.已知二次函数y=ax2+bx+c中x与y的部分对应值如表:
把此函数的图象沿着x轴向右平移1个单位长度后,函数值y=m所对应的x的值为3.
| x | -3 | -2 | 0 | 2 | 3 | 5 | 6 |
| y | 7 | 0 | -8 | m | -5 | 7 | 16 |
20.下列运算正确的是( )
| A. | a6+a3=a9 | B. | a2•a3=a5 | C. | (2a)3=6a3 | D. | (a-b)2=a2-b2 |
4.若关于x的方程x2+bx+1=0有两个不相等的实数根,则a的值可以是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
18. 如图,过点A的一次函数的图象与正比例函数y=3x的图象相交于点B,则这个一次函数的表达式是( )
如图,过点A的一次函数的图象与正比例函数y=3x的图象相交于点B,则这个一次函数的表达式是( )
 如图,过点A的一次函数的图象与正比例函数y=3x的图象相交于点B,则这个一次函数的表达式是( )
如图,过点A的一次函数的图象与正比例函数y=3x的图象相交于点B,则这个一次函数的表达式是( )| A. | y=x+2 | B. | y=2x+5 | C. | y=-x+4 | D. | y=-x+5 |
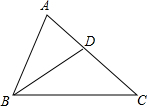 如图,在△ABC中,点D在边AC上,∠ABD=∠ACB,如果S△ABD=4,S△BCD=5,CD=5,那么AB=6米.
如图,在△ABC中,点D在边AC上,∠ABD=∠ACB,如果S△ABD=4,S△BCD=5,CD=5,那么AB=6米.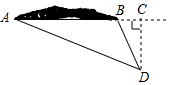 钓鱼岛是我国固有领土,东西长约3641米,如图所示,某海警船巡航到点D处时,测得岛上最东端“东钓角”(A点处)的方向角为北偏西67.5°,最西端“西钓角”(B点处)的方向角为北偏西30°,已知此时海警船到直线AB的距离是2000米,根据以上数据,请求出钓鱼岛东西长度AB的距离,并比较你的计算结果与实际长度的误差(参考数据:tan30°≈0.578,tan67.5°≈2.414,cos30°≈1.732,cot67.5°≈0.414)
钓鱼岛是我国固有领土,东西长约3641米,如图所示,某海警船巡航到点D处时,测得岛上最东端“东钓角”(A点处)的方向角为北偏西67.5°,最西端“西钓角”(B点处)的方向角为北偏西30°,已知此时海警船到直线AB的距离是2000米,根据以上数据,请求出钓鱼岛东西长度AB的距离,并比较你的计算结果与实际长度的误差(参考数据:tan30°≈0.578,tan67.5°≈2.414,cos30°≈1.732,cot67.5°≈0.414)