题目内容
5. 如图,AD是△ABC的中线,线段AC与DE互相平分.
如图,AD是△ABC的中线,线段AC与DE互相平分.(1)求证:四边形ABDE是平行四边形;
(2)若BC=5,AC=4,AB=a,要使四边形ADCE是菱形,求a的值.
分析 (1)根据平行四边形的判定得出四边形ADCE是平行四边形,根据平行四边形的性质求出AE∥DC,AE=DC,求出BD=AE,BD∥AE,根据平行四边形的判定得出即可;
(2)根据菱形的性质得出BD=DC=AD,求出∠BAC=90°,根据勾股定理求出即可.
解答 (1)证明:∵线段AC与DE互相平分,
∴四边形ADCE是平行四边形,
∴AE∥DC,AE=DC,
∵AD是△ABC的中线,
∴BD=DC,
即BD=AE,BD∥AE,
∴四边形ABDE是平行四边形;
(2)解:∵四边形ADCE是菱形,
∴AD=DC=BD,
∴∠BAC=90°,
由勾股定理得:AB=a=$\sqrt{B{C}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
即a=3.
点评 本题考查了菱形的性质,勾股定理,平行四边形的性质和判定的应用,能熟练地运用定理进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.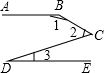 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )
 如图,已知AB∥DE,那么下列结论正确的是( )
如图,已知AB∥DE,那么下列结论正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=180° | C. | ∠1=∠2+∠3 | D. | ∠1-∠2+∠3=180° |
13.若2m2-3m-7=0,7n2+3n-2=0,其中m,n为实数,且mn≠1,则m+$\frac{1}{n}$=( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{2}$ | D. | $-\frac{7}{2}$ |
20.零是( )
| A. | 最小的正数 | B. | 最小的整数 | C. | 最大的负数 | D. | 绝对值最小的数 |
12.一只不透明的袋子中装有5个黑球4个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到白球的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
 如图,在正方形ABCD中,点E在BC上,以AE边作等腰Rt△AEF,∠AEF=90°,AE=EF,FG⊥BC于G.
如图,在正方形ABCD中,点E在BC上,以AE边作等腰Rt△AEF,∠AEF=90°,AE=EF,FG⊥BC于G. 如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.
如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE. 如图所示,三角形ABC是直角三角形,∠ABC=60°,若在直线AC或BC上取一点P,使得三角形PAB为等腰三角形,那么这样的点P的个数为( )
如图所示,三角形ABC是直角三角形,∠ABC=60°,若在直线AC或BC上取一点P,使得三角形PAB为等腰三角形,那么这样的点P的个数为( )