题目内容
8．设x1、x2是方程x2+x-4=0两个实数根，则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{1}{4}$．分析 先根据一元二次方程根与系数的关系确定出x1与x2的两根之积与两根之和的值，再根据$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$即可解答．
解答 解：∵x1、x2是方程x2+x-4=0两个实数根，
∴x1+x2=-1，x1x2=-4，
∵$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$，
∴原式=$\frac{-1}{-4}$=$\frac{1}{4}$，
故答案为：$\frac{1}{4}$．
点评 本题主要考查了根与系数关系的知识，此题将所求的代数式变形后，整体代入求值即可，不需要求得x1、x2的值，此题比较简单．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
如图，四边形ABCD是平行四边形，AB=10，AD=8，AC⊥BC，求AC、OA以及平行四边形ABCD的面积．
19．
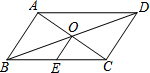如图，?ABCD中，对角线AC，BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（ ）
如图，?ABCD中，对角线AC，BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（ ）| A． | 12cm | B． | 9cm | C． | 6cm | D． | 3cm |
3．
如图，AB是⊙O的直径，∠ABC=30°，OA=6，则扇形AOC面积为（ ）
如图，AB是⊙O的直径，∠ABC=30°，OA=6，则扇形AOC面积为（ ）| A． | 2π | B． | 4π | C． | 6π | D． | 8π |
13．用科学记数法表示0.0000907的结果正确的是（ ）
| A． | 9.1×10-4 | B． | 9.1×10-5 | C． | 9.0×10-5 | D． | 9.07×10-5 |
20．
如图，小“鱼”与大“鱼”是位似图形，已知小“鱼”上一个“顶点”的坐标为（a，b），那么大“鱼”上对应“顶点”的坐标为（ ）
如图，小“鱼”与大“鱼”是位似图形，已知小“鱼”上一个“顶点”的坐标为（a，b），那么大“鱼”上对应“顶点”的坐标为（ ）| A． | （-a，-2b） | B． | （-2a，-b） | C． | （-2a，-2b） | D． | （-b，-2a） |
17．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：
下列结论：（1）ac＜0；（2）当x＞1时，y的值随x值的增大而减小．（3）3是方程ax2+（b-1）x+c=0的一个根；（4）当-1＜x＜3时，ax2+（b-1）x+c＞0．其中正确的个数为（ ）
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -1 | 3 | 5 | 3 | … |
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
18．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
下列结论：
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小；
（3）3是方程ax2+（b-1）x+c=0的一个根；
（4）当x＜-1或x＞3时，ax2+（b-1）x+c＜0．
其中正确的个数为（ ）
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
（1）ac＜0；
（2）当x＞1时，y的值随x值的增大而减小；
（3）3是方程ax2+（b-1）x+c=0的一个根；
（4）当x＜-1或x＞3时，ax2+（b-1）x+c＜0．
其中正确的个数为（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |