题目内容
如图,正方形ABCD中,G为射线BC上一点,连接AG,过G点作GN⊥AG,再作∠DCM的平分线,交GN于点H.
(1)如图1,当G是线段BC的中点时,求证:AG=GH;
(2)如图2,当G是线段BC上任意一点时,(1)中结论还成立吗?若不成立请说明理由;若成立,请写出证明过程.
(3)当G是线段BC的延长线上任意一点时,(1)中结论还成立吗?若不成立请说明理由;若成立,请写出证明过程.
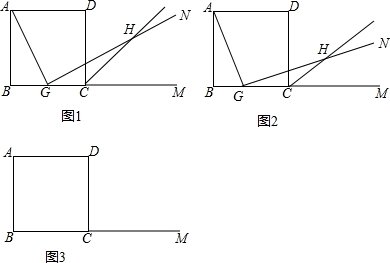
(1)如图1,当G是线段BC的中点时,求证:AG=GH;
(2)如图2,当G是线段BC上任意一点时,(1)中结论还成立吗?若不成立请说明理由;若成立,请写出证明过程.
(3)当G是线段BC的延长线上任意一点时,(1)中结论还成立吗?若不成立请说明理由;若成立,请写出证明过程.

考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)取AB的中点E,连接GE,则GC=AE,由已知可推出∠AEG=∠GCH,∠EAG=∠CGH,从而利用ASA判定△AEG≌△GCH,从而得到AG=GH;
(2)在AB上取一点E,使AE=GC,连接EG,同理可证:△AEG≌△GCH,所以AG=GH;
(3)在BA的延长线上取一点E,使AE=GC,连接EG,同理可证:△AEG≌△GCH,所以AG=GH.
(2)在AB上取一点E,使AE=GC,连接EG,同理可证:△AEG≌△GCH,所以AG=GH;
(3)在BA的延长线上取一点E,使AE=GC,连接EG,同理可证:△AEG≌△GCH,所以AG=GH.
解答:(1)证明:如图1,取AB的中点E,连接GE,则GC=AE.
∵四边形ABCD是正方形,G是线段BC的中点,
∴BG=BE=AE=GC,
∴△BEG为等腰直角三角形,
∴∠AEG=135°,
而CH是∠DCM的平分线,
 ∴∠GCH=135°,
∴∠GCH=135°,
∴∠AEG=∠GCH.
∵AG⊥GH,
∴∠CGH+∠AGB=90°,
又∵∠EAG+∠AGB=90°,
∴∠EAG=∠CGH.
在△AEG与△GCH中,
,
∴△AEG≌△GCH(ASA),
∴AG=GH;
(2)解:当G是线段BC上任意一点时,AG=GH仍成立.理由如下:
如图2,在AB上取一点E,使AE=GC,连接EG.
∵四边形ABCD是正方形,CH平分∠DCM,
∴∠GCH=135°.
∵BE=BG,
∴∠BEG=45°,
∴∠AEG=135°,
∴∠AEG=∠GCH.
∵AG⊥GH,
∴∠CGH+∠AGB=90°,
又∵∠EAG+∠AGB=90°,
∴∠EAG=∠CGH.
在△AEG与△GCH中,
,
∴△AEG≌△GCH(ASA),
∴AG=GH;
(3)解:当G是线段BC的延长线上任意一点时,AG=GH仍成立.理由如下:
如图3,在BA的延长线上取一点E,使AE=GC,连接EG,则BE=BG.
∵∠B=90°,BG=BE,
∴∠AEG=45°,
又∠GCH=45°,
∴∠AEG=∠GCH.
∵∠EAG=90°+∠DAG,∠CGH=90°+∠BGA,
∵AD∥CB,
∴∠DAG=∠BGA,
∴∠EAG=∠CGH.
在△AEG与△GCH中,
,
∴△AEG≌△GCH(ASA),
∴AG=GH.
∵四边形ABCD是正方形,G是线段BC的中点,
∴BG=BE=AE=GC,
∴△BEG为等腰直角三角形,
∴∠AEG=135°,
而CH是∠DCM的平分线,
 ∴∠GCH=135°,
∴∠GCH=135°,∴∠AEG=∠GCH.
∵AG⊥GH,
∴∠CGH+∠AGB=90°,
又∵∠EAG+∠AGB=90°,
∴∠EAG=∠CGH.
在△AEG与△GCH中,
|
∴△AEG≌△GCH(ASA),
∴AG=GH;
(2)解:当G是线段BC上任意一点时,AG=GH仍成立.理由如下:
如图2,在AB上取一点E,使AE=GC,连接EG.
∵四边形ABCD是正方形,CH平分∠DCM,
∴∠GCH=135°.
∵BE=BG,
∴∠BEG=45°,
∴∠AEG=135°,
∴∠AEG=∠GCH.
∵AG⊥GH,
∴∠CGH+∠AGB=90°,
又∵∠EAG+∠AGB=90°,
∴∠EAG=∠CGH.
在△AEG与△GCH中,
|
∴△AEG≌△GCH(ASA),
∴AG=GH;
(3)解:当G是线段BC的延长线上任意一点时,AG=GH仍成立.理由如下:
如图3,在BA的延长线上取一点E,使AE=GC,连接EG,则BE=BG.
∵∠B=90°,BG=BE,
∴∠AEG=45°,
又∠GCH=45°,
∴∠AEG=∠GCH.
∵∠EAG=90°+∠DAG,∠CGH=90°+∠BGA,
∵AD∥CB,
∴∠DAG=∠BGA,
∴∠EAG=∠CGH.
在△AEG与△GCH中,
|
∴△AEG≌△GCH(ASA),
∴AG=GH.
点评:此题主要考查了正方形的性质、角平分线的性质及全等三角形的判定与性质,正确作出辅助线,构造三角形全等是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△ABC中AB=13,BC=14,AC=15,BC边上高为AD,求△ABC的面积.
如图,△ABC中AB=13,BC=14,AC=15,BC边上高为AD,求△ABC的面积.
 在Rt△ABC中,∠ACB=90°,若CA=8,BC=6,点D、E分别是AC、AB的中点.则DE=
在Rt△ABC中,∠ACB=90°,若CA=8,BC=6,点D、E分别是AC、AB的中点.则DE=