题目内容
16. 如图,在平行四边形ABCD中,AB=5cm,BC=8cm,∠B=60°,G是CD的中点,E是边AD上的动点EG的延长线与BC的延长线交于点F,连结CE,DF.
如图,在平行四边形ABCD中,AB=5cm,BC=8cm,∠B=60°,G是CD的中点,E是边AD上的动点EG的延长线与BC的延长线交于点F,连结CE,DF.(1)求证:四边形CEDF是平行四边形;
(2)当AE=5.5cm时,四边形CEDF是矩形.
分析 (1)欲证明四边形CEDF是平行四边形,只要证明CG=GD,GF=GE或CF=ED即可.
(2)当CE⊥AD时,四边形CEDF是矩形,在RT△CED中求出ED即可解决问题.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴CF∥ED,ED,
∴∠FCG=∠EDG,
∵G是CD的中点,
∴CG=DG,
∵∠CGF=∠DGE,
∴△FCG≌△EDG,
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形.
(2)解:当CE⊥AD时,∠CED=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
在RT△CED中,∵CD=AB=5,∠DCE=∠B=60°,
∴ED=$\frac{1}{2}$CD=$\frac{5}{2}$,
∵AD=BC=8,
∴AE=AD-ED=8-$\frac{5}{2}$=5.5.
故答案为5.5.
点评 本题考查平行四边形的性质、矩形的判定和性质、直角三角形30度角性质等知识,解题的关键是熟练掌握平行四边形的判定和性质以及矩形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目
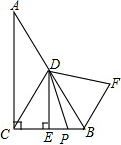 【探究】如图,在Rt△ABC中,∠ACB=90°,∠A=30°CD是AB边上的中线,DE⊥BC于E.P是线段CB上一点,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BC、BF、BP三者之间的数量关系,并证明你的结论.
【探究】如图,在Rt△ABC中,∠ACB=90°,∠A=30°CD是AB边上的中线,DE⊥BC于E.P是线段CB上一点,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BC、BF、BP三者之间的数量关系,并证明你的结论. 如图,点M在∠AOB的边OB上.
如图,点M在∠AOB的边OB上.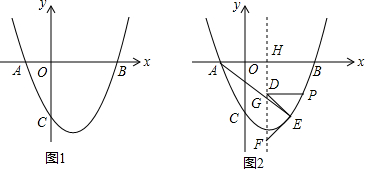 在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC. 中,字母x的取值范围是( )
中,字母x的取值范围是( ) B.
B.  C.
C.  D.
D. 
 如图,将BM′绕点O按逆时针方向旋转45°后得到△A′OB′,若△AOB=15°,则∠AOB′的度数是30°.
如图,将BM′绕点O按逆时针方向旋转45°后得到△A′OB′,若△AOB=15°,则∠AOB′的度数是30°.