题目内容
16.顺次连结任意对角线互相垂直的四边形各边中点所得到的四边形一定是( )| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
分析 根据三角形中位线的性质,可得到这个四边形是平行四边形,再由对角线垂直,能证出有一个角等于90°,则这个四边形为矩形.
解答 解:是矩形,理由如下:
如图,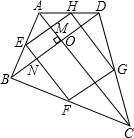 AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.
AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.
∵E、F、G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD(三角形的中位线平行于第三边),
∴四边形EFGH是平行四边形(两组对边分别平行的四边形是平行四边形),
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形(有三个角是直角的四边形是矩形),
∴∠MEN=90°,
∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).
故选:B.
点评 本题考查了中点四边形三角形的中位线定理的应用,熟练掌握三角形中位线定理以及矩形的各种判定方法是解题关键.

练习册系列答案
相关题目
7.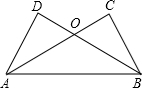 如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
 如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )
如图,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC与BD相交于点O,如果AC=BD,那么下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD中正确的有( )| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ②③ |
4.下列各式从左至右属于因式分解的是( )
| A. | x2-9+8x=(x+3)(x-3)+8x | B. | (x+3)(x-3)+8x=x2-9+8x | ||
| C. | (a+b)(a-b)=a2-b2 | D. | a2-2a(b-c)-3(b-c)2=(a-3b+3c)(a+b-c) |
1.下列长度的3根小棒,能搭成三角形的是( )
| A. | 9,5,2 | B. | 5,4,9 | C. | 4,6,9 | D. | 8,5,13 |
5.一个两位数,个位数字为b,十位数字为a,则这个两位数为( )
| A. | a b | B. | b a | C. | 10a+b | D. | 10b+a |
 (1)若a,b两数在数轴上的表示如下:
(1)若a,b两数在数轴上的表示如下: 如图,矩形内有两个相邻的正方形,面积分别为4和a2,那么阴影部分的面积为2a-a2.
如图,矩形内有两个相邻的正方形,面积分别为4和a2,那么阴影部分的面积为2a-a2.