题目内容
15.为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为每个40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(个)与销售单价x(元)满足一次函数关系:y=-10x+1200.(1)求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额-成本);
(2)该公司当地物价部门规定,商品售价不得高于成本的1.9倍,当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?
分析 (1)根据“总利润=单件的利润×销售量”列出二次函数关系式即可;
(2)将得到的二次函数配方后即可确定最大利润,再结合二次函数增减性得出答案.
解答 解:(1)由题意可得:S=(x-40)(-10x+1200)=-10x2+1600x-48000;
(2)S=-10x2+1600x-48000
=-10(x-80)2+16000
依题意:x≤40×1.9,
即x≤76,
对于二次函数S=-10(x-80)2+16000,
当x≤80时,s随x的增大而增大,
故当x最大为76时,s最大为15840元.
点评 此题主要考查了二次函数的性质在实际生活中的应用,最大销售利润的问题常利函数的增减性来解答,要注意应该在自变量的取值范围内求最大值(或最小值).

练习册系列答案
相关题目
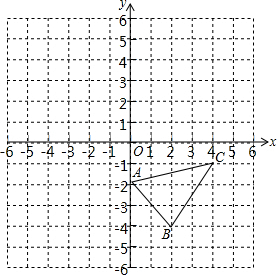 如图,平面直角坐标系中△ABC,分别画出与△ABC关于x轴、y轴对称的△A1B1C1和△A2B2C2,并写出△A1B1C1和△A2B2C2各顶点坐标.
如图,平面直角坐标系中△ABC,分别画出与△ABC关于x轴、y轴对称的△A1B1C1和△A2B2C2,并写出△A1B1C1和△A2B2C2各顶点坐标.