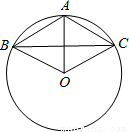
题目内容
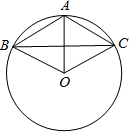 如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm
如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm(1)求证:∠AOB=∠AOC;
(2)求圆片的半径R(结果保留根号);
(3)若在(2)题中的R的值满足n<R<m(其中m、n为正整数),试估算m的最小值和n的最大值.
分析:(1)由AB=AC,根据弧、圆心角、弦的关系,即可证得:∠AOB=∠AOC;
(2)由垂径定理,可求得BD的长,然后由勾股定理求得AD的长,继而可得方程:R2=(R-
)2+25,解此方程即可求得答案;
(3)首先估计
的取值范围,则可求得R的取值范围,继而求得答案.
(2)由垂径定理,可求得BD的长,然后由勾股定理求得AD的长,继而可得方程:R2=(R-
| 11 |
(3)首先估计
| 11 |
解答:(1)证明:∵AB=AC,
∴
=
,
∴∠AOB=∠AOC;
(2)解:设OA交BC于点D,
∵
=
,
∴OA⊥BC,
∴BD=
BC=
×10=5(cm),
∵AB=6cm,
∴在Rt△ABD中,AD=
=
(cm),
∵OB=Rcm,
则OD=(R-
)cm,
∵OB2=OD2+BD2,
∴R2=(R-
)2+25,
解得:R=
(cm);
(3)∵3<
<4,
∴4<
<6
∴m=6,n=4.
∴
 |
| AB |
 |
| AC |
∴∠AOB=∠AOC;
(2)解:设OA交BC于点D,
∵
 |
| AB |
 |
| AC |
∴OA⊥BC,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=6cm,
∴在Rt△ABD中,AD=
| AB2-BD2 |
| 11 |
∵OB=Rcm,
则OD=(R-
| 11 |
∵OB2=OD2+BD2,
∴R2=(R-
| 11 |
解得:R=
| 18 |
| 11 |
| 11 |
(3)∵3<
| 11 |
∴4<
| 18 |
| 11 |
| 11 |
∴m=6,n=4.
点评:此题考查了垂径定理,圆心角、弧弦的关系以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
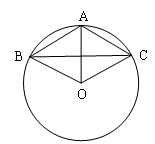
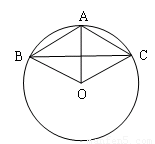
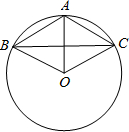 如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm
如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm