题目内容
5. 如图,△ABC≌△CDA,则下列结论错误的是( )
如图,△ABC≌△CDA,则下列结论错误的是( )| A. | ∠1=∠2 | B. | AB=CD | C. | ∠B=∠D | D. | AC=BC |
分析 根据“全等三角形的对应角相等、对应边相等”的性质进行判断并作出正确的选择.
解答 解:A、∠1与∠2是全等三角形△ABC≌△CDA的对应角,则∠1=∠2,故本选项不符合题意;
B、线段AB与CD是全等三角形△ABC≌△CDA的对应边,则AB=CD,故本选项不符合题意;
C、∠B与∠D是全等三角形△ABC≌△CDA的对应角,则∠B=∠D,故本选项不符合题意;
D、线段AC与BC不是全等三角形△ABC≌△CDA的对应边,则AC≠BC,故本选项符合题意;
故选:D.
点评 本题考查了全等三角形的性质.利用全等三角形的性质时,一定要找对对应角和对应边.

练习册系列答案
相关题目
20.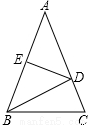 如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
 如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )| A. | 15cm | B. | 10cm | C. | 8cm | D. | 5cm |
17.下列运算正解的是( )
| A. | $\sqrt{5}$+$\sqrt{7}$=$\sqrt{12}$ | B. | 5+$\sqrt{2}$=5$\sqrt{2}$ | C. | $\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{{(-2)}^{2}}$=-2 |
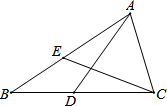 如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.
如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.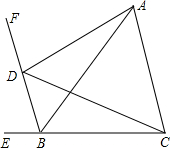 已知,BF平分△ABC的外角ABE,D为BF上一动点.
已知,BF平分△ABC的外角ABE,D为BF上一动点.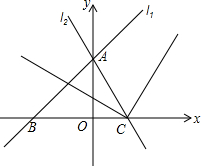 如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.
如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.