题目内容
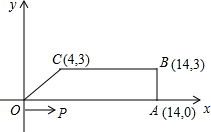 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿OC、CB以每秒2个单位向终点B运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿OC、CB以每秒2个单位向终点B运动.当这两点中有一点到达自己的终点时,另一点也停止运动.(1)设从出发起运动了x秒,且x>2.5时,Q点的坐标;
(2)当x等于多少时,四边形OPQC为平行四边形?
(3)四边形OPQC能否成为等腰梯形?说明理由;
(4)设四边形OPQC的面积为y,求出当x>2.5时y与x的函数关系式;并求出y的最大值.
分析:根据题意可分别列出Q点在OC段,CB段的函数关系式和P点在DA上的关系式,按要求进行解答即可.
解答:解:先求出各个点到终点需要的时间:
∵C(4,3),
∴OC=
=5,
∵B(14,3),
∴BC=14-4=10,
∴t(Q)=
=
,
t(P)=14,
(1)由题意可知,当x>2.5时,Q点在CB上运动,
故横坐标为2x-5+4=2x-1,纵坐标为3,故坐标为(2x-1,3);
(2)由平行四边形的对边相等可知,2x-5=x,解得x=5;
(3)不能,OPQC成为等腰梯形的条件是P跑到Q的前面去,且x>2.5这时的Q和O关系为
p的横坐标-Q的横坐标=4,
于是列方程:1×x=4+2×(x-2.5)+4,
解得x=-3(舍去),
故OPQC不能成为等腰梯形.
(4)当x>2.5时,四边形OPQC是一个梯形,所以:
y=
=
因为x最大为7.5,而根据上面的函数式知道y随x的增大而增大,
所以当x为最大时y为最大.
所以,y最大=3×
=26.25.
∵C(4,3),
∴OC=
| 42+32 |
∵B(14,3),
∴BC=14-4=10,
∴t(Q)=
| 5+14-4 |
| 2 |
| 15 |
| 2 |
t(P)=14,
(1)由题意可知,当x>2.5时,Q点在CB上运动,
故横坐标为2x-5+4=2x-1,纵坐标为3,故坐标为(2x-1,3);
(2)由平行四边形的对边相等可知,2x-5=x,解得x=5;
(3)不能,OPQC成为等腰梯形的条件是P跑到Q的前面去,且x>2.5这时的Q和O关系为
p的横坐标-Q的横坐标=4,
于是列方程:1×x=4+2×(x-2.5)+4,
解得x=-3(舍去),
故OPQC不能成为等腰梯形.
(4)当x>2.5时,四边形OPQC是一个梯形,所以:
y=
| 3(2x-5+x) |
| 2 |
| 3(3x-5) |
| 2 |
因为x最大为7.5,而根据上面的函数式知道y随x的增大而增大,
所以当x为最大时y为最大.
所以,y最大=3×
| 3×7.5-5 |
| 2 |
点评:要求学生对直角梯形有一定的掌握,并对点在图形中的运动函数的熟练运用.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
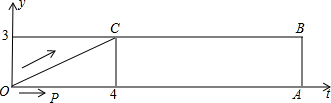 出相应的t的值和P、Q的坐标;如不可能,请说明理由.
出相应的t的值和P、Q的坐标;如不可能,请说明理由. 正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形ABCD重叠的面积为S(平方单位).
正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形ABCD重叠的面积为S(平方单位). 如图,梯形OABC中,BC∥AO,∠BAO=90°,B(-3
如图,梯形OABC中,BC∥AO,∠BAO=90°,B(-3 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为