题目内容
如图,梯形OABC中,CB∥OA,O为坐标原点,A(4,0),C(0,4),tan∠BAO=2,动点P从点C出发,以每秒1个单位的速度沿线段CB运动到点B后,再以每秒
个单位的速度沿线段BA运动,到点A停止,过点P作PQ⊥x轴于Q,以PQ为一边向左作 正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形ABCD重叠的面积为S(平方单位).
正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形ABCD重叠的面积为S(平方单位).
(1)求点B的坐标.
(2)求S与t的函数关系式.
(3)求(2)中的S的最大值.
(4)连接OB,OB中点为M,正方形PQRS在变化过程中,使点M在正方形PQRS的边上的t值为
| 5 |
 正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形ABCD重叠的面积为S(平方单位).
正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形ABCD重叠的面积为S(平方单位).(1)求点B的坐标.
(2)求S与t的函数关系式.
(3)求(2)中的S的最大值.
(4)连接OB,OB中点为M,正方形PQRS在变化过程中,使点M在正方形PQRS的边上的t值为
1秒或3秒
1秒或3秒
.分析:(1)过B作BD垂直于x轴于D点,由C的坐标得出OC的长,再由A的坐标得出OA的长,根据四边形BDOC为矩形,得到对边相等,即BC=OD,BD=OC,在直角三角形ABD中,利用锐角三角函数定义表示出tan∠BAO,根据tan∠BAO=2及BD的长,求出AD的长,同时利用勾股定理求出AB的长,由OA-AD求出OD的长,由BD与OD的长,及B在第一象限,写出B的坐标即可;
(2)根据P的位置分三种情况考虑:(i)当P在BC边上时,正方形PQRS与梯形ABCD重叠的面积为矩形PQOC的面积,而PQ=OC=4,CP=t,表示出S与t的关系式,并写出此时t的范围;(ii)当P在AB边上,且S在y轴左侧时,如图所示,P在BC边上运动的时间是2秒,P在BA边上运动由时间(t-2)秒,根据P每秒
个单位的速度沿线段BA运动,利用路程=时间×速度,表示出BP的长,由AB-BP表示出AP,在直角三角形APQ中,由tan∠BAO=2,设AQ=x,则有PQ=2x,利用勾股定理表示出AP,列出关于x的方程,求出方程的解表示出AQ与PQ,由OA-AQ求出OQ的长,由矩形的两条边OQ与PQ的乘积即可得出S与t的关系式,并写出此时t的范围;当P在AB边上,且S在y轴右侧时,如图所示,此时重合部分为正方形PQRS,由表示出的PQ,即可表示出此时S与t的关系式,并求出此时t的范围;
(3)由(2)得出的S与t的关系式,利用一次函数及二次函数的性质求出三个函数的最大值,比较后即可求出S的最大值;
(4)分两种情况考虑:(i)当P在BC边上时,若PQ过M点,由M为OB的中点,得到BM=OM,再由BC与OA平行,利用两直线平行得到两对内错角相等,利用AAS可得出三角形PBM与三角形OMQ全等,利用全等三角形的对应边相等得到PB=OQ,而OQ=CP=t,得到CP=PB,PB=CB-CP=2-t,列出关于t的方程,求出方程的解即可得到t的值;(ii)当P在AB边上运动时,此时S与M重合,由M为OB的中点,MP平行于OA,利用平行线等分线段定理得到P为AB的中点,即MP为三角形AOB的中位线,利用中位线定理得到MP为OA的一半,求出MP的长,即为此时正方形的边长,由PQ=8-2t,令8-2t等于求出的边长列出关于t的方程,求出方程的解即可得到此时t的值.
(2)根据P的位置分三种情况考虑:(i)当P在BC边上时,正方形PQRS与梯形ABCD重叠的面积为矩形PQOC的面积,而PQ=OC=4,CP=t,表示出S与t的关系式,并写出此时t的范围;(ii)当P在AB边上,且S在y轴左侧时,如图所示,P在BC边上运动的时间是2秒,P在BA边上运动由时间(t-2)秒,根据P每秒
| 5 |
(3)由(2)得出的S与t的关系式,利用一次函数及二次函数的性质求出三个函数的最大值,比较后即可求出S的最大值;
(4)分两种情况考虑:(i)当P在BC边上时,若PQ过M点,由M为OB的中点,得到BM=OM,再由BC与OA平行,利用两直线平行得到两对内错角相等,利用AAS可得出三角形PBM与三角形OMQ全等,利用全等三角形的对应边相等得到PB=OQ,而OQ=CP=t,得到CP=PB,PB=CB-CP=2-t,列出关于t的方程,求出方程的解即可得到t的值;(ii)当P在AB边上运动时,此时S与M重合,由M为OB的中点,MP平行于OA,利用平行线等分线段定理得到P为AB的中点,即MP为三角形AOB的中位线,利用中位线定理得到MP为OA的一半,求出MP的长,即为此时正方形的边长,由PQ=8-2t,令8-2t等于求出的边长列出关于t的方程,求出方程的解即可得到此时t的值.
解答:解:(1)过B作BD⊥x轴于D点,如图所示:

由C(0,4),得到OC=4,由A(4,0),得到OA=4,
∵四边形BDOC为矩形,∴BC=OD,BD=OC=4,
在Rt△ABD中,tan∠BAO=
=2,AB=
=2
,
解得:AD=2,
∴OD=OA-AD=4-2=2,
∴B(2,4);
(2)分三种情况考虑:
(i)当P点在BC边上运动时,由题意得:CP=t,
又四边形PQOC为矩形,∴PQ=OC=4,
则正方形PQRS与梯形ABCD重叠的面积为S=CP•PQ=4t(0≤t≤2);
(ii)当P在BA边上运动时(S在y轴左侧),如图所示:

由题意得:BP=
(t-2),又AB=2
,
∴AP=AB-BP=2
-
(t-2)=
(4-t),
在Rt△APQ中,tan∠BAO=
=2,设AQ=x,则PQ=2x,
根据勾股定理得:AP=
x,又AP=
(4-t),
∴
x=
(4-t),即x=4-t,
∴AQ=4-t,PQ=8-2t,
∴OQ=OA-AQ=4-(4-t)=t,
则正方形PQRS与梯形ABCD重叠的面积为S=OQ•PQ=t(8-2t)=-2t2+8t(2≤t<
);
(iii)当P在BA边上运动时(S在y轴右侧),如图所示:

同理得到PQ=8-2t,此时重合部分为正方形PQRS,
则S=PQ2=(8-2t)2=4t2-32t+64(
≤t<4);
(3)由(2)列出的函数关系式,分三种情况考虑:
(i)S=4t(0≤t≤2),由一次函数为增函数,故当t=2时,S最大=8;
(ii)S=-2t2+8t(2<t<
),此时S没有最大值;
(iii)S=4t2-32t+64(
≤t<4),由二次函数性质得:当t=
时,S=
,
由
<8,得到问题(2)中的S的最大值是8;
(4)分两种情况考虑:
(i)当P在BC边上,且PQ过M点时,如图所示:

∵M为OB中点,
∴BM=OM,
又BC∥OA,
∴∠BPM=∠MQO,∠PBM=∠QOM,
∴△BPM≌△OQM(AAS),
∴PB=OQ,又OQ=CP=t,CB=2,
∴PB=2-t,即2-t=t,
解得:t=1;
(ii)当P在AB边上,且SR过M点时(此时S与M重合),如图所示:

∵M为OB的中点,MP∥OA,
∴P为AB中点,即MP为△AOB的中位线,
∴MP=
OA=2,即正方形PQRS的边长为2,
由PQ=8-2t,得到8-2t=2,
解得:t=3,
综上,点M在正方形PQRS的边上的t值为1秒或3秒.
故答案为:1秒或3秒

由C(0,4),得到OC=4,由A(4,0),得到OA=4,
∵四边形BDOC为矩形,∴BC=OD,BD=OC=4,
在Rt△ABD中,tan∠BAO=
| BD |
| AD |
| BD2+AD2 |
| 5 |
解得:AD=2,
∴OD=OA-AD=4-2=2,
∴B(2,4);
(2)分三种情况考虑:
(i)当P点在BC边上运动时,由题意得:CP=t,
又四边形PQOC为矩形,∴PQ=OC=4,
则正方形PQRS与梯形ABCD重叠的面积为S=CP•PQ=4t(0≤t≤2);
(ii)当P在BA边上运动时(S在y轴左侧),如图所示:

由题意得:BP=
| 5 |
| 5 |
∴AP=AB-BP=2
| 5 |
| 5 |
| 5 |
在Rt△APQ中,tan∠BAO=
| PQ |
| AQ |
根据勾股定理得:AP=
| 5 |
| 5 |
∴
| 5 |
| 5 |
∴AQ=4-t,PQ=8-2t,
∴OQ=OA-AQ=4-(4-t)=t,
则正方形PQRS与梯形ABCD重叠的面积为S=OQ•PQ=t(8-2t)=-2t2+8t(2≤t<
| 8 |
| 3 |
(iii)当P在BA边上运动时(S在y轴右侧),如图所示:

同理得到PQ=8-2t,此时重合部分为正方形PQRS,
则S=PQ2=(8-2t)2=4t2-32t+64(
| 8 |
| 3 |
(3)由(2)列出的函数关系式,分三种情况考虑:
(i)S=4t(0≤t≤2),由一次函数为增函数,故当t=2时,S最大=8;
(ii)S=-2t2+8t(2<t<
| 8 |
| 3 |
(iii)S=4t2-32t+64(
| 8 |
| 3 |
| 8 |
| 3 |
| 64 |
| 9 |
由
| 64 |
| 9 |
(4)分两种情况考虑:
(i)当P在BC边上,且PQ过M点时,如图所示:

∵M为OB中点,
∴BM=OM,
又BC∥OA,
∴∠BPM=∠MQO,∠PBM=∠QOM,
∴△BPM≌△OQM(AAS),
∴PB=OQ,又OQ=CP=t,CB=2,
∴PB=2-t,即2-t=t,
解得:t=1;
(ii)当P在AB边上,且SR过M点时(此时S与M重合),如图所示:

∵M为OB的中点,MP∥OA,
∴P为AB中点,即MP为△AOB的中位线,
∴MP=
| 1 |
| 2 |
由PQ=8-2t,得到8-2t=2,
解得:t=3,
综上,点M在正方形PQRS的边上的t值为1秒或3秒.
故答案为:1秒或3秒
点评:此题属于相似形综合题,涉及的知识有:全等三角形的判定与性质,坐标与图形性质,锐角三角函数定义,勾股定理,正方形的性质,三角形的中位线定理,以及一次函数与二次函数的性质,利用了数形结合及分类讨论的数学思想,是一道较难的压轴题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
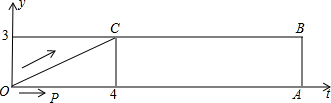 出相应的t的值和P、Q的坐标;如不可能,请说明理由.
出相应的t的值和P、Q的坐标;如不可能,请说明理由.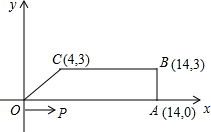 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿OC、CB以每秒2个单位向终点B运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿OC、CB以每秒2个单位向终点B运动.当这两点中有一点到达自己的终点时,另一点也停止运动. 如图,梯形OABC中,BC∥AO,∠BAO=90°,B(-3
如图,梯形OABC中,BC∥AO,∠BAO=90°,B(-3 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为