题目内容
 如图,梯形OABC中,BC∥AO,∠BAO=90°,B(-3
如图,梯形OABC中,BC∥AO,∠BAO=90°,B(-3| 3 |
| 3 |
(1)求证:点O1在x轴上;
(2)将点O1运动到点M(-4
| 3 |
(3)在(2)的条件下,将直线MC向下平移m个单位长度,设直线MC与线段AB交于点P,与线段OC的交于点Q,四边形OAPQ的面积为S,求S与m的函数关系式,并求出m的取值范围.
分析:(1)根据特殊角的三角形函数值、旋转的性质以及等边三角形的判定推知△COO1为等边三角形,则∠COA=∠COO1=60°,即OA与OO1在同一直线上,所以点O1在x轴上.
(2)由旋转的性质、坐标与图形是性质易证B1、C、O三点共线.然后根据点B、C的坐标以及直角梯形的性质证得MC是等腰三角形B1MO的中垂线,最后由等腰三角形“三合一”的性质求得∠B1MC=
∠BMO=30°;
(3)根据图形知,S四边形OAPQ=S梯形PAQN+S△QNO.然后由梯形的面积公式和三角形的面积公式进行计算.由PQ与边AB有交点来求m的取值范围.
(2)由旋转的性质、坐标与图形是性质易证B1、C、O三点共线.然后根据点B、C的坐标以及直角梯形的性质证得MC是等腰三角形B1MO的中垂线,最后由等腰三角形“三合一”的性质求得∠B1MC=
| 1 |
| 2 |
(3)根据图形知,S四边形OAPQ=S梯形PAQN+S△QNO.然后由梯形的面积公式和三角形的面积公式进行计算.由PQ与边AB有交点来求m的取值范围.
解答: (1)证明:如图1,∵BC∥AO,B(-3
(1)证明:如图1,∵BC∥AO,B(-3
,3),
∴点C的纵坐标是3,
又∵直线OC的解析式为y=-
x,
∴3=-
x,
解得,x=-
,则C(-
,3)
∴tan∠COA=
,
∴∠COA=60°.
∵根据旋转的性质知,∠OCO1=60°,CO=CO1
∴△COO1为等边三角形,
∴∠COO1=60°
∴∠COA=∠COO1
∴点O1在x轴上.
(2)解:如图2,∵∠COO1=60°,BC∥AO,
∴∠BCO=120°,
∴B1CO1=120°.
∵∠O1CO=60°,
∴∠B1CO=180°,
∴B1、C、O三点共线.
∵C(-
,3),
∴CO=CO1=O1O=2
,
∵MO=4
,
∴MO1=O1O=O1C,
可证得∠MCO=90°
∵BC=CO=2
,BC=B1C,
∴B1C=CO,
∴MB1=MO,
∴∠B1MC=
∠BMO=30°;
(3)解:如图3,设MC与AB边交于点D,过点C作CE∥AB交PQ于点E,过点Q作QN⊥OA于点N.
∵AD=1,PD=m,
∴AP=1-m.
在△CEQ中,CE=m,∠ECQ=30°
∴CQ=
m,
∴OQ=2
-
m
∴QN=3-
m,ON=
-
m
∴AN=2
+
m
又∵S四边形OAPQ=S梯形PAQN+S△QNO
∴S=
+
(
-
m)(3-
m)
∴S=-
m2-2
m+
(0<m<1)
 (1)证明:如图1,∵BC∥AO,B(-3
(1)证明:如图1,∵BC∥AO,B(-3| 3 |
∴点C的纵坐标是3,
又∵直线OC的解析式为y=-
| 3 |
∴3=-
| 3 |
解得,x=-
| 3 |
| 3 |
∴tan∠COA=
| 3 |
∴∠COA=60°.
∵根据旋转的性质知,∠OCO1=60°,CO=CO1
∴△COO1为等边三角形,
∴∠COO1=60°
∴∠COA=∠COO1
∴点O1在x轴上.
(2)解:如图2,∵∠COO1=60°,BC∥AO,
∴∠BCO=120°,
∴B1CO1=120°.
∵∠O1CO=60°,
∴∠B1CO=180°,

∴B1、C、O三点共线.
∵C(-
| 3 |
∴CO=CO1=O1O=2
| 3 |
∵MO=4
| 3 |
∴MO1=O1O=O1C,
可证得∠MCO=90°
∵BC=CO=2
| 3 |
∴B1C=CO,
∴MB1=MO,
∴∠B1MC=
| 1 |
| 2 |
(3)解:如图3,设MC与AB边交于点D,过点C作CE∥AB交PQ于点E,过点Q作QN⊥OA于点N.
∵AD=1,PD=m,

∴AP=1-m.
在△CEQ中,CE=m,∠ECQ=30°
∴CQ=
| ||
| 2 |
∴OQ=2
| 3 |
| ||
| 2 |
∴QN=3-
| ||
| 4 |
| 3 |
| ||
| 4 |
∴AN=2
| 3 |
| ||
| 4 |
又∵S四边形OAPQ=S梯形PAQN+S△QNO
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| ||
| 4 |
∴S=-
| ||
| 8 |
| 3 |
| 11 |
| 2 |
| 3 |
点评:本题考查了一次函数的综合题.此题涉及的知识点比较多:一次函数图象上点的坐标特征,等边三角形的判定与性质,等腰三角形的性质,梯形的面积公式以及三角形的面积公式等.解答(3)题时,注意“分割法”的应用.

练习册系列答案
相关题目
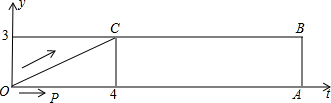 出相应的t的值和P、Q的坐标;如不可能,请说明理由.
出相应的t的值和P、Q的坐标;如不可能,请说明理由.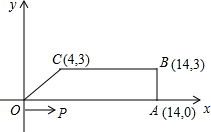 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿OC、CB以每秒2个单位向终点B运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿OC、CB以每秒2个单位向终点B运动.当这两点中有一点到达自己的终点时,另一点也停止运动. 正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形ABCD重叠的面积为S(平方单位).
正方形PQRS,设运动时间为t(秒),正方形PQRS与梯形ABCD重叠的面积为S(平方单位). 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为