题目内容
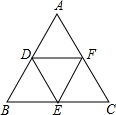
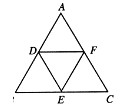
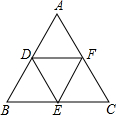 如图,分别取等边三角形ABC各边的中点D,E,F,得△DEF.若△ABC的边长为a.
如图,分别取等边三角形ABC各边的中点D,E,F,得△DEF.若△ABC的边长为a.(1)△DEF与△ABC相似吗?如果相似,相似比是多少?
(2)分别求出这两个三角形的面积.
(3)这两个三角形的面积比与边长之比有什么关系?
分析:(1)先证明出△DEF是等边三角形,两等边三角形相似,进而求出相似比;
(2)根据三角形的面积公式求出这两个三角形的面积;
(3)算出两个三角形的面积比与边长之比,再得到结论.
(2)根据三角形的面积公式求出这两个三角形的面积;
(3)算出两个三角形的面积比与边长之比,再得到结论.
解答:解:(1)∵D、E、F分别是△ABC的边AB、BC、AC的中点,
∴DE=
AC,DF=
BC,EF=
AB,
∵等边三角形ABC,
∴△DEF是等边三角形,
∴△DEF与△ABC相似,相似比是
,
(2)S△ABC=
×a×
a=
a2,
S△DEF=
×
a×
a2=
a2.
(3)两个三角形的面积比为1:4,边长之比为1:2,
三角形的面积比等于边长之比的平方.
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵等边三角形ABC,
∴△DEF是等边三角形,
∴△DEF与△ABC相似,相似比是
| 1 |
| 2 |
(2)S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
S△DEF=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 16 |
(3)两个三角形的面积比为1:4,边长之比为1:2,
三角形的面积比等于边长之比的平方.
点评:本题考查了相似三角形的判定与性质:平行于三角形一边的直线截其它两边所得的三角形与原三角形相似;相似三角形对应边的比相等.

练习册系列答案
相关题目
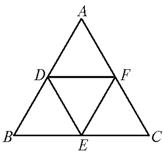
 如图,分别取等边三角形ABC各边的中点D,E,F,得△DEF.若△ABC的边长为a.
如图,分别取等边三角形ABC各边的中点D,E,F,得△DEF.若△ABC的边长为a.