题目内容
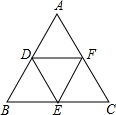
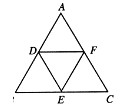
如图:分别取等边三角形ABC各边的中点D、E、F,得△DEF.若△ABC的边长为a.
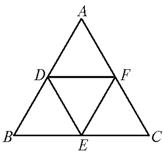
(1)△DEF与△ABC相似吗?如果相似,相似比是多少?
(2)分别求出这两个三角形的面积;
(3)这两个三角形的面积比与边长之比有什么关系吗?
【答案】
(1)相似,相似比为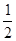 ;
;
(2)△ABC的面积为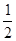 AB·AE=
AB·AE=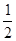 a·
a·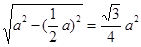
△DEF的面积为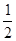 ·
·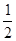 a·
a·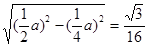 a2;
a2;
(3)则这两个三角形的面积比等于边长之比的平方.
【解析】
试题分析:(1)根据三角形中位线定理可得DE=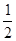 a,EF=DF=
a,EF=DF=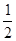 a,即可得到△DEF是等边三角形,从而得到结果;
a,即可得到△DEF是等边三角形,从而得到结果;
(2)根据等边三角形的性质结合三角形的面积公式即可求得结果;
(3)根据这两个三角形的面积比与边长之比的值即可判断.
(1)根据三角形中位线定理得DE=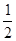 a,EF=DF=
a,EF=DF=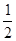 a
a
所以△DEF是等边三角形,
所以△DEF与△ABC相似,相似比为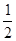 ;
;
(2)△ABC的面积为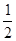 AB·AE=
AB·AE=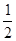 a·
a·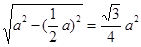
△DEF的面积为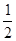 ·
·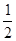 a·
a·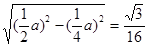 a2;
a2;
(3)S△DEF∶S△ABC=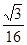 a2∶
a2∶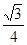 a2=
a2=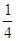 ∶1=1∶4
∶1=1∶4
则这两个三角形的面积比等于边长之比的平方.
考点:三角形中位线定理,等边三角形的性质,相似三角形的判定与性质
点评:相似三角形的判定在中考中往往不以单独的知识点出现,而是出现在综合性的大题中,如二次函数与圆的应用等问题,因而熟练掌握相似三角形的判定方法极为重要.

练习册系列答案
相关题目
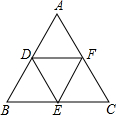 如图,分别取等边三角形ABC各边的中点D,E,F,得△DEF.若△ABC的边长为a.
如图,分别取等边三角形ABC各边的中点D,E,F,得△DEF.若△ABC的边长为a. 如图,分别取等边三角形ABC各边的中点D,E,F,得△DEF.若△ABC的边长为a.
如图,分别取等边三角形ABC各边的中点D,E,F,得△DEF.若△ABC的边长为a.