题目内容
 如图,AB是半圆O的直径,AD和BC是它的两条切线,OD平分∠ADC.
如图,AB是半圆O的直径,AD和BC是它的两条切线,OD平分∠ADC.(1)求证:CD是⊙O的切线.
(2)若AB=10cm,AD=xcm,BC=ycm(x、y>0).
①求y关于x的函数关系式;
②试用x表出两个阴影部分的面积之和S阴影,并探索S阴影是否存在最小值,写出探索过程.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)利用角平分线的性质结合切线的判定方法得出即可;
(2)①利用切线长定理以及勾股定理得出y与x的函数关系式即可;
②利用2S阴影=S四边形ABCD-S半圆面积,进而得出S与x的函数关系,再利用配方法求出最值即可.
(2)①利用切线长定理以及勾股定理得出y与x的函数关系式即可;
②利用2S阴影=S四边形ABCD-S半圆面积,进而得出S与x的函数关系,再利用配方法求出最值即可.
解答:(1)证明:过点O作OE⊥DC于点E,
∵AB是半圆O的直径,AD和BC是它的两条切线,
∴∠BAD=90°,
∵OD平分∠ADC,
∴AO=OE,
∴CD是⊙O的切线;
(2)解:①过点D作DF⊥BC于点F,
∵AD,CD是⊙O的切线,E为切点,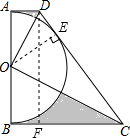
∴BC=EC,AD=DE,
∵AB=10cm,AD=xcm,BC=ycm(x、y>0),
∴DF=10,DC=x+y,FC=y-x,
则DF2+FC2=DC2,
即102+(y-x)2=(x+y)2,
整理得:100=4xy,
则y=
;
②由题意可得:2S阴影=S四边形ABCD-S半圆面积=
(x+y)×10-
π×25=5(x+
)-
,
故S阴影=
(x+
)-
π=
[(
-
)2+10]-
=
(
-
)2+25-
,
故当
-
=0时,S阴影最小为25-
.
∵AB是半圆O的直径,AD和BC是它的两条切线,
∴∠BAD=90°,
∵OD平分∠ADC,
∴AO=OE,
∴CD是⊙O的切线;
(2)解:①过点D作DF⊥BC于点F,
∵AD,CD是⊙O的切线,E为切点,

∴BC=EC,AD=DE,
∵AB=10cm,AD=xcm,BC=ycm(x、y>0),
∴DF=10,DC=x+y,FC=y-x,
则DF2+FC2=DC2,
即102+(y-x)2=(x+y)2,
整理得:100=4xy,
则y=
| 25 |
| x |
②由题意可得:2S阴影=S四边形ABCD-S半圆面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| x |
| 25π |
| 2 |
故S阴影=
| 5 |
| 2 |
| 25 |
| x |
| 25 |
| 4 |
| 5 |
| 2 |
| x |
| 5 | ||
|
| 25π |
| 4 |
| 5 |
| 2 |
| x |
| 5 | ||
|
| 25π |
| 4 |
故当
| x |
| 5 | ||
|
| 25π |
| 4 |
点评:此题主要考查了切线的判定以及切线长定理以及配方法求最值,得出S与x的函数关系是解题关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
下列说法正确的是( )
| A、8的立方根是±2 | ||
B、
| ||
| C、1的平方根是1 | ||
D、
|
 在某种运算编程的程序中,如图,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12…那么第2014次输出的结果为
在某种运算编程的程序中,如图,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12…那么第2014次输出的结果为 如图,已知线段b、c、m,求作△ABC,使它的两边分别等于b和c,第三边上的中线等于m.
如图,已知线段b、c、m,求作△ABC,使它的两边分别等于b和c,第三边上的中线等于m. 已知,如图∠ABD=∠EBC,∠BAD=∠BCE,求证:△DEB∽△ABC.
已知,如图∠ABD=∠EBC,∠BAD=∠BCE,求证:△DEB∽△ABC. 如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm,
如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=xcm,