题目内容
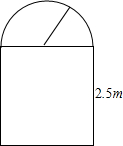
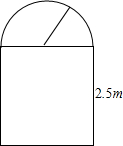 一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为2.5m.
一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为2.5m.(1)求隧道截面的面积S(m2)与上半部半径r(m)的函数关系式.
(2)求当上部半圆半径为2m的截面面积.
分析:(1)已知圆的半径为r,可知矩形的另一边长为2r,分别计算半圆面积和矩形面积,列出函数关系式;
(2)把r=2代入函数关系式,可求面积.
(2)把r=2代入函数关系式,可求面积.
解答:解:(1)圆的半径为r,矩形的另一边长为2r,
则:隧道截面的面积S=
πr2+2r×2.5,
即S=
πr2+5r;
(2)当r=2时,截面面积为
S=
×π×22+5×2=2π+10(m2).
则:隧道截面的面积S=
| 1 |
| 2 |
即S=
| 1 |
| 2 |
(2)当r=2时,截面面积为
S=
| 1 |
| 2 |
点评:本题考查了利用面积法列函数关系式的方法,并要求会对函数式进行简单的运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
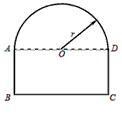
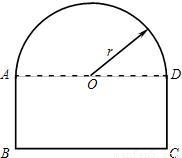
 一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD.
一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD.