题目内容
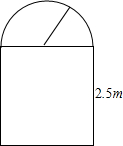
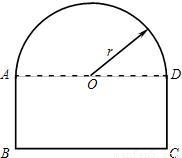
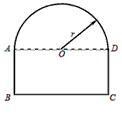
一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD。
⑴当AD=4米时,求隧道截面上部半圆O的面积;
⑵已知矩形ABCD相邻两边之和为8米,半圆O的半径为r米。
①求隧道截面的面积S(米2)关于半径r(米)的函数关系式(不要求写出r的取值范围);
②若2米≤CD≤3米,利用函数图象求隧道截面的面积S的最大值(π取3.14,结果精确到0.1米)
⑴当AD=4米时,求隧道截面上部半圆O的面积;
⑵已知矩形ABCD相邻两边之和为8米,半圆O的半径为r米。
①求隧道截面的面积S(米2)关于半径r(米)的函数关系式(不要求写出r的取值范围);
②若2米≤CD≤3米,利用函数图象求隧道截面的面积S的最大值(π取3.14,结果精确到0.1米)
解:(1)当AD=4米时,S半圆= =2π(米2)
=2π(米2)
(2)①∵AD=2r,AD+CD=8,
∴CD=8-AD=8-2r,
∴S= =
= ;
;
②由①知CD=8-2r,
又∵2米≤CD≤3米,
∴2≤8-2r≤3,
∴2.5≤r≤3,
由①知S= =-2.43r2+16r=
=-2.43r2+16r= ,
,
∵-2.43<0,
∴函数图象为开口向下的抛物线,
∵函数对称轴r= ≈3.3,
≈3.3,
又2.5≤r≤3<3.3,
由函数图象知,在对称轴左侧S随的增大而增大,
故当r=3时,有S最大值,
 ≈
≈ =26.13≈26.1(米2)
=26.13≈26.1(米2)
答:隧道截面的面积S的最大值约为26.1米2。
 =2π(米2)
=2π(米2)(2)①∵AD=2r,AD+CD=8,
∴CD=8-AD=8-2r,
∴S=
 =
= ;
;②由①知CD=8-2r,
又∵2米≤CD≤3米,
∴2≤8-2r≤3,
∴2.5≤r≤3,
由①知S=
 =-2.43r2+16r=
=-2.43r2+16r= ,
,∵-2.43<0,
∴函数图象为开口向下的抛物线,
∵函数对称轴r=
 ≈3.3,
≈3.3,又2.5≤r≤3<3.3,
由函数图象知,在对称轴左侧S随的增大而增大,
故当r=3时,有S最大值,
 ≈
≈ =26.13≈26.1(米2)
=26.13≈26.1(米2)答:隧道截面的面积S的最大值约为26.1米2。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD.
一条隧道的截面如图所示,它的上部是一个以AD为直径的半圆O,下部是一个矩形ABCD.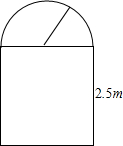 一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为2.5m.
一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为2.5m.