题目内容
 如图,在△ABC和△DEF中,AB=DE,∠ACB=∠EFD,点B,C,F,E在同一条直线上,且AB∥DE.求证:BF=CE.
如图,在△ABC和△DEF中,AB=DE,∠ACB=∠EFD,点B,C,F,E在同一条直线上,且AB∥DE.求证:BF=CE.考点:全等三角形的判定与性质
专题:证明题
分析:由AB与DE平行,利用两直线平行内错角相等得到一对角相等,再由∠ACB=∠EFD,AB=DE,利用AAS得出△ABC≌△DEF,利用全等三角形的对应边相等得到BC=EF,等式两边都加上CF,即可得到BF=EC.
解答:证明:∵AB∥DE,
∴∠B=∠E,
在△ABC和△EFD中,
,
∴△ABC≌△DEF(AAS),
∴BC=EF,
∴BC+CF=EF+CF,即BF=CE.
∴∠B=∠E,
在△ABC和△EFD中,
|
∴△ABC≌△DEF(AAS),
∴BC=EF,
∴BC+CF=EF+CF,即BF=CE.
点评:此题考查了全等三角形的判定与性质,以及平行线的性质,其中全等三角形的判定方法有:SSS;SAS;ASA;AAS,以及HL(直角三角形判定全等的方法).

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,在正方形纸片ABCD中,E为BC的中点.折叠正方形,使点A与点E重合,压平后得折痕MN.设梯形ADMN的面积为S1,梯形BCMN的面积为S2,则
如图,在正方形纸片ABCD中,E为BC的中点.折叠正方形,使点A与点E重合,压平后得折痕MN.设梯形ADMN的面积为S1,梯形BCMN的面积为S2,则| S1 |
| S2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知mn≠1,且5m2+2009m+9=0,9n2+2009n+5=0,则
的值为( )
| m |
| n |
| A、-402 | ||
B、
| ||
C、
| ||
D、
|
在下列实数中,无理数是( )
| A、-2 | ||
B、
| ||
C、
| ||
| D、π |
 正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°
正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°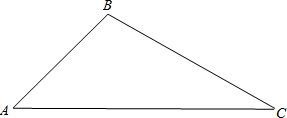 规作图确定医院M的位置.(不要求写出作法、证明,但要保留作图痕迹,请务必用铅笔作图).
规作图确定医院M的位置.(不要求写出作法、证明,但要保留作图痕迹,请务必用铅笔作图).