题目内容
 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,给出以下四个结论:①AE=CF;
②△EPF是等腰直角三角形;
③S四边形AEPF=
| 1 |
| 2 |
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),EF的最小值等于BC的一半.
上述结论中始终正确的有( )
| A、①④ | B、①② |
| C、①②③ | D、①②③④ |
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:利用旋转的思想观察全等三角形,寻找条件证明三角形全等.根据全等三角形的性质对题中的结论逐一判断.
解答: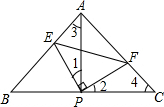 解:∵∠APE、∠CPF都是∠APF的余角,
解:∵∠APE、∠CPF都是∠APF的余角,
∴∠1=∠2,
∵AB=AC,∠BAC=90°,P是BC中点,
∴AP=CP,
在△APE与△CPF中,
,
∴△APE≌△CPF(ASA),
同理可证△APF≌△BPE,
①由△APE≌△CPF得到AE=CF,故①正确;
②由△APE≌△CPF得到PE=PF,
∵∠EPF是直角,
∴△EPF是等腰直角三角形,故②正确;
③由△APE≌△CPF得到S△APE=S△CPF,则S四边形AEPF=S△AEP+S△APF=S△CPF+S△APF=
S△ABC,故③正确;
④∵AB=AC,∠BAC=90°,
∴AB=
BC,
由②知,△EPF是等腰直角三角形,则EF=
EP.当EP⊥AB时,EP去最小值,此时EP=
AB,则EF最小值=
AB=
•
BC=
BC.故④正确;
综上所述,正确的结论是①②③④,共有4个.
故选D.
 解:∵∠APE、∠CPF都是∠APF的余角,
解:∵∠APE、∠CPF都是∠APF的余角,∴∠1=∠2,
∵AB=AC,∠BAC=90°,P是BC中点,
∴AP=CP,
在△APE与△CPF中,
|
∴△APE≌△CPF(ASA),
同理可证△APF≌△BPE,
①由△APE≌△CPF得到AE=CF,故①正确;
②由△APE≌△CPF得到PE=PF,
∵∠EPF是直角,
∴△EPF是等腰直角三角形,故②正确;
③由△APE≌△CPF得到S△APE=S△CPF,则S四边形AEPF=S△AEP+S△APF=S△CPF+S△APF=
| 1 |
| 2 |
④∵AB=AC,∠BAC=90°,
∴AB=
| ||
| 2 |
由②知,△EPF是等腰直角三角形,则EF=
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
综上所述,正确的结论是①②③④,共有4个.
故选D.
点评:此题主要考查了全等三角形的判定与性质,涉及到等腰三角形和直角三角形的性质,难度适中.

练习册系列答案
相关题目
下列各数:
,π,
,0.1010010001…(相邻两个“1”之间依次多一个“0”),其中无理数有
( )
| 1 |
| 2 |
| 3 | -27 |
( )
| A、0个 | B、1个 | C、2个 | D、3个 |
将点P(-3,2)向右平移2个单位后,向下平移3个单位得到点Q,则点Q的坐标为( )
| A、(-5,5) |
| B、(-1,-1) |
| C、(-5,-1) |
| D、(-1,5) |
下列计算正确的是( )
| A、-1-1=0 | ||
| B、(-3)2=6 | ||
C、
| ||
| D、3×(-2)=-6 |
若25x2-mxy+9y2是一个完全平方式,那么m的值为( )
| A、15 | B、±15 |
| C、30 | D、±30 |
不改变分式的值,下列变化正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
计算:(-
)-1的值是( )
| 2 |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、±
|