Question

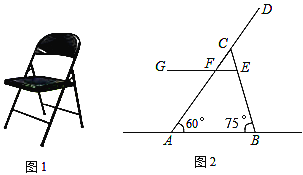
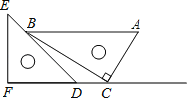
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置，点C在FD的延长线上，点B在ED上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，AC＝10，则CD的长度是_____.

Answer 1

【答案】15﹣5.

【解析】

过点B作BM⊥FD于点M，根据题意可求出BC的长度，然后在△EFD中可求出∠EDF＝45°，进而可得出答案.

过点B作BM⊥FD于点M，

在△ACB中，∠ACB＝90°，∠A＝60°，AC＝10，

∴∠ABC＝30°，BC＝10×tan60°＝10，

∵AB∥CF，

∴∠BCM=∠ABC=30°，

∴BM＝BC×sin30°＝＝5，

CM＝BC×cos30°＝15，

在△EFD中，∠F＝90°，∠E＝45°，

∴∠EDF＝45°，

∴MD＝BM＝5，

∴CD＝CM﹣MD＝15﹣5，

故答案是：15﹣5.